Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 10ª Edição - Russel C. Hibbeler- Ed: 10º - Capítulo 2.6 - Ex. 67

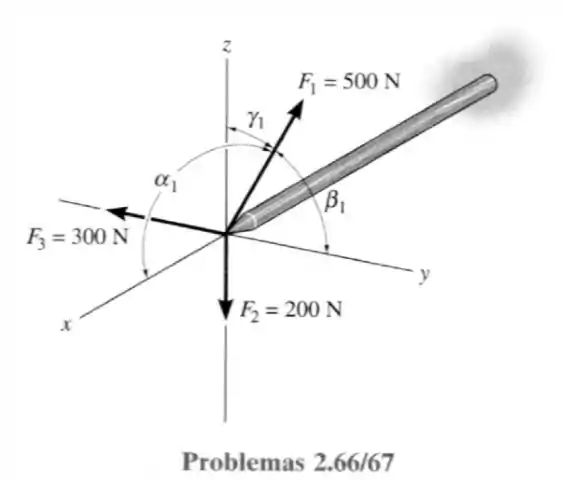
67- O mastro está sujeito as três forças mostradas. Determine os ângulos diretores coordenados α 1 , β 1 , γ 1 de F 1 , de modo que a força resultante que atua sobre o mastro seja nula.

Passo 1

A diferença da questão passada é que a igualdade da força resultante será:

500 cos ⁡ α 1 i + ( 500 cos ⁡ β 1 - 300 ) j + 500 cos ⁡ γ 1 - 200 k = 0 i + 0 j + 0 k

Uma vez que as forças continuam iguais.

Logo teremos:

500 cos ⁡ α 1 = 0 → α 1 = cos - 1 ⁡ 0 = 90 °

Agora:

500 cos ⁡ β 1 - 300 = 0

β 1 = cos - 1 ⁡ 300 500 = 53.1 °

E :

500 cos ⁡ γ 1 - 200 = 0

γ 1 = cos - 1 ⁡ 200 500 = 66.4 °

Resposta

α 1 = 90 °

β 1 = 53.1 °

γ 1 = 66.4 °

Ver Outros Exercícios desse livro