Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 72
72- Usando o método da Seção , resolva o Problema
Passo 1
Viga do Problema .
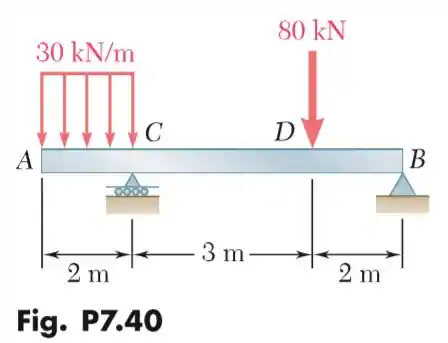
O que se pede.
Para a viga e o carregamento mostrados na figura, trace os diagramas de esforço cortante e do momento fletor determine os valores absolutos máximos do esforço cortante e do momento fletor.
Sabendo que o apoio em é de primeiro gênero e somente reage na vertical e que em temos uma reação nos dois sentidos. E que o carregamento de gera um força resultante de:
E que ela dista de do apoio em , nos dando a seguinte viga equivalente.
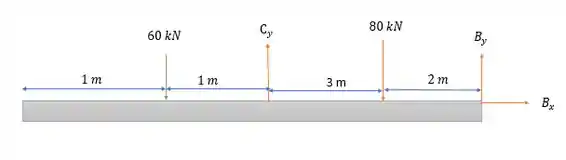
Fazendo a somatória das forças horizontais nós temos:
Fazendo a somatória das forças verticais nós temos:
E agora fazendo a somatória dos momentos em :
Dessa forma:
Passo 2
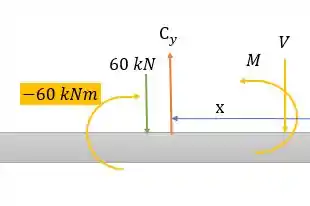
Vamos traçar o diagrama de cortante e de momento fletor, começando da seção :
Pela somatória das forças verticais nós temos:
Equação de uma reta.
Onde para nós temos um cortante igual a:
E agora o momento fletor:
Onde para temos um momento fletor igual a:
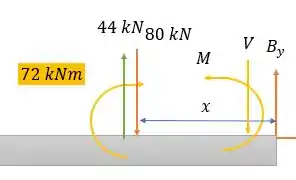
Aproveitando então o momento fletor resultante e a cortante vamos avançar para a seção de :
Fazendo a somatória das forças verticais temos:
E a somatória dos momentos nos dará:
Isso nos dará:
Onde que para temos:
Agora no intervalo de :
Fazendo a somatória das forças verticais nós encontraremos uma cortante igual a:
Valor que se anula com .
Para os momentos .
Onde para temos .
Dessa forma encontramos o maior cortante absoluto igual a e o maior momento absoluto igual a
Passo 3
Diagrama da cortante:
Agora o diagrama do momento fletor:
Note que a área do triângulo da cortante nos dá o momento fletor no final da seção, assim como as áreas dos retângulos com o eixo nos dão os valores ao final das seções seguintes.