Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 29

O Comprimento original da mola é r. Quando o pino P está em uma posição arbitrária θ , determine as componentes x e y da força que a mola exerce no pino. Avalie sua expressão para r = 400 mm, k = 1,4 kN/m e θ = 40°. (Nota: força em uma mola é dada por F = k   δ , em que δ é a extensão do comprimento original.)

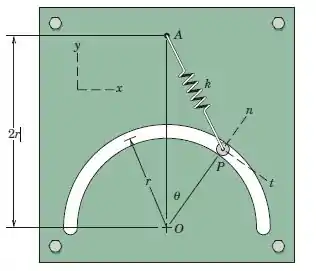
Passo 1

Para separar a força entre os eixos será necessário descobrir o ângulo que a força F fax com o eixo y ou x. Vamos cumprir esse desafio separando a figura em dois triângulos retângulos.

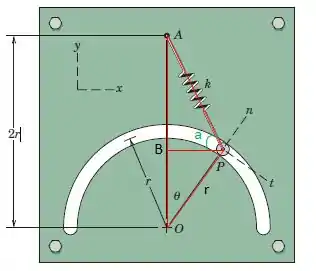
Passo 2

Descobrir o valor do ângulo a :

Para isso precisamos obter o valor dos lados do triangulo superior.

Então vamos calcular o tamanho de cada segmento:

  A O - =   2 r

B O - = r c o s ( θ )

  B P - = r s e n ( θ )

A B - = A O - -   B O - =   2 r -   r c o s θ = r [ 2 - c o s θ ]

A P - 2 =   B P - 2 + A B - 2   →     A P - =   [ r s e n θ ] 2 + r 2 - c o s θ 2  

Como A P - cos ⁡ a =   B P -  

a = cos - 1 ⁡ B P - A P - = cos - 1 ⁡ r s e n θ [ r s e n θ ] 2 + r 2 - c o s θ 2

Substituindo os valores de θ = 40 ° e r = 400   m m   obtemos a = 62,4 ° .

!!!Fica ligado se sua calculadora está em radianos ou graus. Para converter de graus para radianos basta multiplicar o valor em graus por π e dividir por 180.

Passo 3

Calcular F x e F y . Começamos esse paço calculando o valor de δ .

Como δ é o deslocamento da mola que estava inicialmente a distância r. δ =   A P - -   r .

Logo δ =   [ r s e n θ ] 2 + r 2 - c o s θ 2 - r = 157   m m , para de θ = 40 ° e r = 400   m m  

Agora temos tudo para calcular o valor da força nos eixos x e y.

F x = - F cos ⁡ a = - k δ cos ⁡ a

F y =   F s e n ( a ) = - k δ sen ⁡ a  

Substituindo os valores de k = 1400   N / m   , δ = 0,157   m e a = 62,4 ° obtemos:

F x = - 101,5   N

F y = 194,4   N

Resposta

F x = - 101,5   N

F y = 194,4   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As três forças atuam perpendicular a placa retangular como mostrado. Determine os momentos M 1 deF 1 ,M 2d eF 2eM 3d eF 3 , todos relacionados ao ponto O .
A tensão no suporte do cabo B Cé3200N é . Escreva a força que este cabo exerce sobre a longarina O A B como um vetor T . Determine os ângulos θ x ,θ yeθ zque a linha de ação de T formam com os eixos p
A viga H , de aço, foi projetada como uma coluna para suportar as duas forças verticais, como mostrado. Substitua essas forças por uma força equivalente simples ao longo da linha de centro vertical da
O tensionador é apertado até que a força trativa no cabo A B seja de 1,2k N . Calcule a magnitude do módulo em relação ao ponto O da força atuando no ponto A .
Uma cantoneira é soldada na extremidade da viga I para suportar uma força de 35k N , aplicada paralelamente ao eixo da viga, e uma força de 20 kN, aplicada na extremidade da viga. Ao analisar a capaci