Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 96
Determine a área da seção transversal exigida para o elemento e os diâmetros exigidos para os pinos em e se a tensão normal admissível for e a tensão de cisalhamento for .
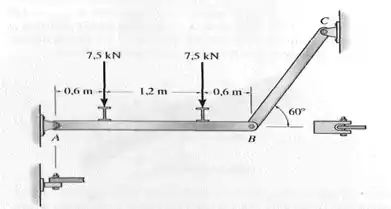
Passo 1
Oláaaa, querido! Cê está bem?
A gente quer encontrar a área da seção transversal exigida por e ainda a dimensão dos diâmetros dos pinos em e em , para isso precisamos saber todas as forças envolvidas no problema, assim vamos começar calculando as reações dos suportes.
Depois vamos aplicar as equações da tensão cisalhante, porque se trata de pinos sofrendo cisalhamento.
E também vamos aplicar a expressão da tensão normal para a barra , que tem como carregamento uma força axial , responsável por ajudar no suporte da barra .
E para que a gente vai fazer isso tudo? Para achar essas medidas das peças que ele pediu.
Boraaa
Passo 2
Vamos aplicar as equações de equilíbrio na barra de forma isolada inicialmente. Adotando o sentido anti-horário como positivo temos
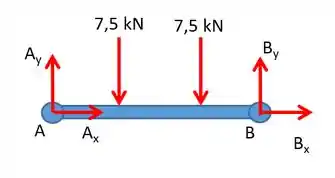
Passo 3
A força na barra tem componente horizontal e vertical, como já encontramos sua componente vertical podemos usá-la para descobrir o valor da força , já que sabemos o ângulo que faz com a horizontal:
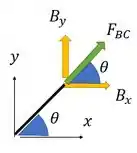
A gente sabe que está nesse sentido porque ela segura um dos lados da barra . Daí da figura a gente tem que
Além disso, temos pela figura que
Passo 4
Agora vamos fazer o somatório das forças em :
Finalmente em :
Mais tarde vamos precisar do módulo da força então vamos calcular logo aqui:
Passo 5
Agora, temos todas as forças que precisamos para calcular o que o exercício pede. Vamos começar pela área do elemento . Podemos achar a área da seção transversal de uma barra pela expressão da tensão normal é dada por
Para a barra
Percebe que a gente quer a área para que ela aguente a força sabendo que esse elemento tem tensão normal máxima permitida de . Então a gente substitui essas coisas ali em cima:
Observe que utilizamos a força em e a tensão em assim o resultado será em
Passo 6
Agora vamos usar a expressão de tensões de cisalhamento para achar o diâmetro dos pinos:
Os pinos tem seção transversal circular, né? Então a área é
Substituindo na expressão da tensão:
Isolando o diâmetro:
Sendo que é a força paralela a seção, a força interna resultante de cisalhamento.
Passo 7
Agora muita calma, vamos refletir. Repara no pino em . Quem é a força paralela a seção transversal dele? Cara, a seção transversal dele está no plano da nossa folha que a gente fez o DCL, então a força de cisalhamento para ele também está no plano da folha.
Aí quem atua no ponto e está no plano da folha? Issso mesmo, a . Mas antes de dizer que , a gente precisa ver o cisalhamento é duplo ou simples.
Repara no detalhe que ele fez para o pino . Vamos fazer uma réplica lindona aqui mostrando as forças atuando nele:
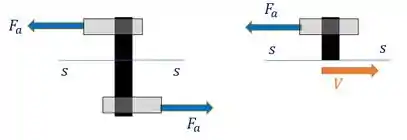
Temos uma placa que liga ele a barra e outra que liga ele a parede. Nessas duas placas, a força é a força , para que o pino fique em equilíbrio na sua horizontal; Então se a gente faz uma seção no pino (desenho da direita), vemos que
Ou seja, temos cisalhamento simples. E o nosso diâmetro fica:
Passo 8
Agora vamos ver o detalhe do pino B:
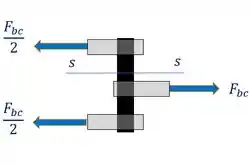
A força paralela a sua seção transversal é . Só que repara que ela é exercida por essa placa do meio. E para acoplar o pino a barra AB, são usadas duas placas nas extremidades. Para que haja o equilíbrio horizonta do pino, a força dessas duas placas da barra AB precisam ser .
Vamos fazer uma seção para achar . Aonde? Cara, a gente vai fazer ali onde está marcado , mas se fizer no intervalo de baixo, dá na mesma. Vamos ficar assim:
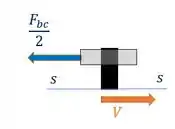
Percebe que
E isso acontece exatamente porque o pino é acoplado a barra AB por duas placas. Ou seja, ele está sofrendo cisalhamento duplo. Então nosso diâmetro aqui fica: