Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 12.Problemas - Ex. 137
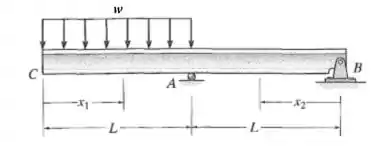
Determine a deflexão máxima entre os apoios A e B. EI é constante. Use o método da integração.
Passo 1
Fala aí pessoal, partiu mais um problema de resmat. A gente precisa determinar a deflexão em AB máxima. Precisamos então das equações da linha elástica.
Repara que ele pediu para usarmos o método da integração. Então vamos achar uma equação para CA e outra para AB.
Primeira coisa a fazer é achar as reações de apoio. Supondo que a reação em A está para cima e a em B está para baixo, podemos usar as equações de equilíbrio:
Agora, devemos ulizar as equações de equilíbrio:
Passo 2
Sabemos que a equação da linha elástica e sua inclinação podem ser obtidas determinando o momento interno no elemento em função de . Neste caso, temos várias cargas agindo e, por isso, devemos integrar . Ao integrar uma vez, otemos a equação para a inclinação da linha elástica, e integrando novamente, obtemos a equação para a deflexão.
Para , temos:
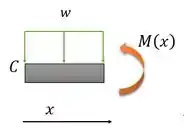
Passo 3
Para
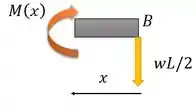
Passo 4
Com isso, temos as condições de contorno. São elas:
Isso porque nos apoios, temos deflexão nula.
Já as condições de continuidade são:
Porque em pontos iguais da barra, precisamos ter valores iguais para ambas as equações.
Substituindo as condições de contorno na equação, temos:
Resolvendo esse sistema:
Passo 5
Por fim, para que a deflexão entre os apoios A e B seja máxima, , já que é a função para deflexão em AB. Sendo assim:
E solucionando a equação temos que . Por isso, substituindo em , temos: