Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 10ª Edição - Russel C. Hibbeler- Ed: 10º - Capítulo 6.3 - Ex. 7
7- Determine a força em cada elemento da treliça e indique se esses elementos estão sob tração ou compressão.
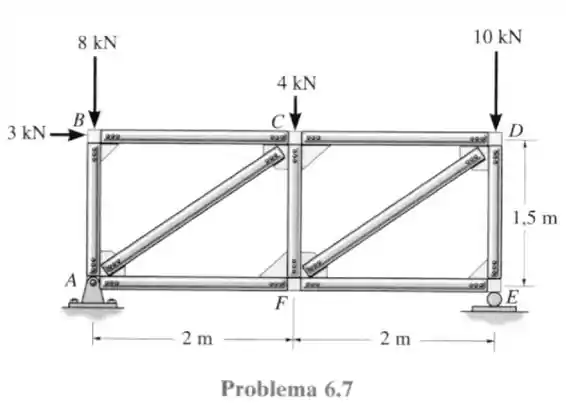
Passo 1
Para resolver essa questão vamos primeiro calcular as reações nos apoios, sabendo que em temos reações verticais e horizontais e em temos somente reação vertical. O que nos dá o seguinte diagrama de forças.
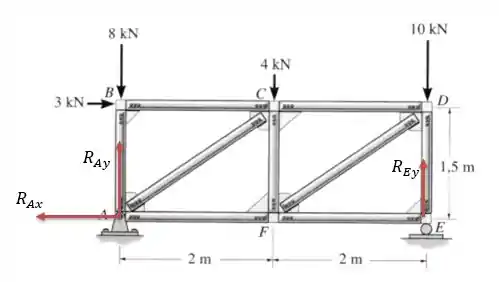
Fazendo a somatória das forças verticais temos:
Agora fazendo a somatória das forças verticais:
E escolhendo o ponto para fazer a somatória de momentos temos (considerando o sentido horário como positivo):
Logo:
Passo 2
Agora que temos todas as forças ativas no sistema, chegou a hora de calcular as forças nas barras e para isso precisamos escolher o nó onde temos o maior numero de forças conhecidas para o menor numero de forças desconhecidas. Um nó um bom para começar é o nó que terá o seguinte diagrama de forças sobre ele.
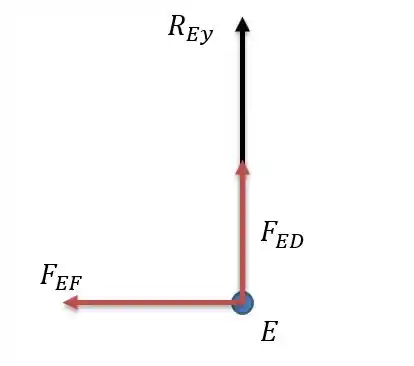
Fazendo a somatória das forças horizontais nós vamos ter:
E a somatória das forças verticais será:
Que pelo sinal e pela abordagem da força sair do nó (que será abordada durante todo o exercício) é um força compressiva. Além de que será a mesma coisa que .
Passo 3
Aquecido? Agora escolhe o ponto ou , bem eu escolhi o para dificultar as coisas um pouco, então vamos lá:
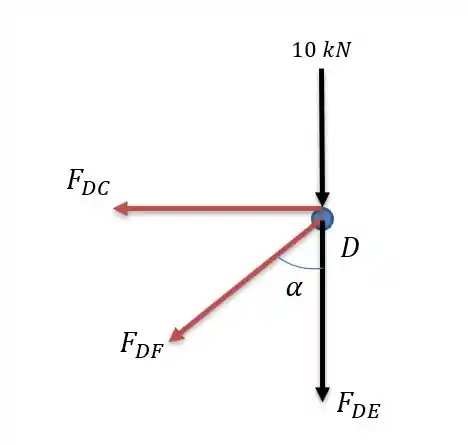
Onde é calculado pelo catetos do triângulo a qual ela pertence:
Fazendo a somatória das forças verticais temos:
Como sabemos do passo anterior temos:
Uma força trativa.
Agora para a somatória das forças horizontais:
Uma força compressiva.
Passo 4
Já temos 4 forças, isso é bem legal já, o passo natural seria agora ir para o nó ou o nó , mas não vamos fazer bullying com o tadinho, já foi descartado da última vez.
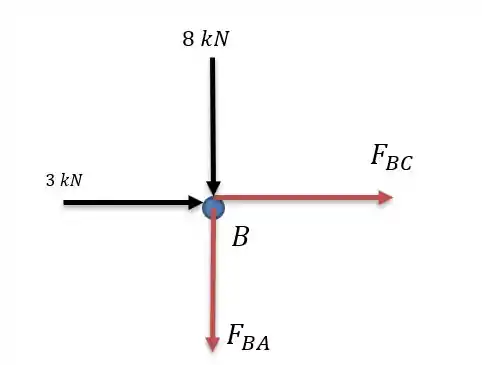
Tem nem graça né, pela somatória das forças horizontais temos:
E pela somatória das verticais:
Ambas forças compressivas.
Passo 5
Agora estou afim de dificultar vou para o nó
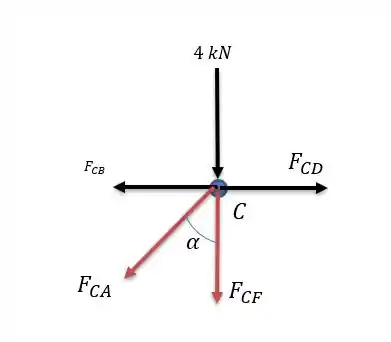
Não sei se deu para perceber, mas as forças que conhecemos estou marcando de preto e as que não conheço de vermelho, e além das forças conhecemos o valor de que é , faó isso para facilitar a nossa vida mesmo.
Se fizermos a somatória das forças horizontais temos que será:
Substituindo:
Com isso encontramos:
Força compressiva.
Agora para a somatória das forças verticais:
Lembrando que leva o sinal negativo, por que estamos adotando o mesmo padrão para todo mundo.
Passo 6
Agora vamos fazer o nó .
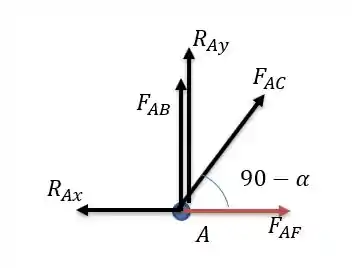
Fazendo a somatória das forças horizontais temos:
Substituindo o que conhecemos temos:
Força trativa.
A partir daqui já começa a surgir oportunidade para verificar se os valores que calculamos até agora estão certos, se fizermos a somatória das forças verticais temos que encontrar zero.
O que dará aproximadamente zero.
Passo 7
Na pegada de averiguar as forças que encontramos podemos calcular a resultante no nó , se a somatória horizontal e vertical derem zero estará tudo correto.
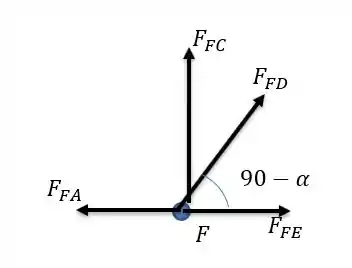
Fazendo a somatória das forças verticais:
E:
Logo está tudo certinho.