Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 7.Problemas - Ex. 103
Determine a força necessária para manter o cabo na posição mostrada, ou seja, de modo que o segmento permaneça horizontal. Além disso, calcule a flecha e a tração máxima no cabo
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Temos aqui nesta questão, para um cabo submetido a três cargas concentradas diferentes, precisamos determinar qual a força que mantém o segmento na horizontal.
Além disto, devemos determinar também a flecha e a tração máxima no cabo (calcular a tração em cada trecho e identificar o maior valor).
Bom, para que possamos fazer isto tudo, esta questão nos dará um pouco de trabalho, pois temos que utilizar o método dos nós para cada um dos pontos , e .
Mas, para isto, vamos utilizar o fato de que as trações nas cordas estão na direção das mesmas!
Sendo assim, vamos para as contas.
Passo 2
Como o nosso objetivo é analisar o equilíbrio em torno de cada nó, vamos começar analisando o nó . Esboçando o seu diagrama de corpo livre, temos:
Aplicando as equações de equilíbrio, temos:
Reorganizando o sistema, temos:
E aí vamos deixar elas paradas momentaneamente e vamos para o nó .
Passo 3
Agora vamos repetir o procedimento para o nó . Esboçando o seu diagrama de corpo livre, temos:
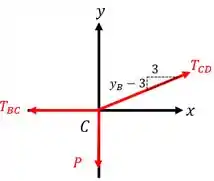
Aplicando as equações de equilíbrio, temos:
Reorganizando as equações, temos:
E aí novamente vamos deixar elas paradas momentaneamente, e partir para o nó .
Passo 4
Agora vamos repetir o procedimento para o nó D. Esboçando o seu diagrama de corpo livre, temos:
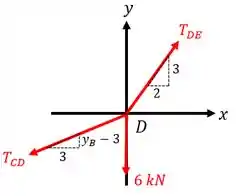
Aplicando as equações de equilíbrio, temos:
Reorganizando as equações, temos:
E assim terminamos de trabalhar com todos os nós.
Passo 5
Agora é só juntarmos todas as relações que nós obtivemos nos Passos 2, 3 e 4 e resolvemos o sistema. Relembrando as equações, temos:
Juntando a primeira, terceira e sexta equação nós obtemos:
Agora que obtivemos o valor de é só sair substituindo nas equações do nosso sistema para encontrar o valor da força e da máxima tração no cabo (obter todas as trações e depois escolher o maior valor). Portanto,
Portanto, .
E assim finalizamos a questão!