Se o cabo está submetido a uma tração de , determine a tração nos cabos e e a intensidade da força vertical .
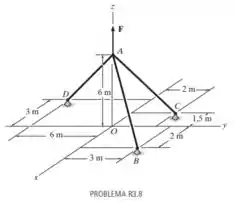
Passo 1
Oi pessoal? Vamos para mais um exercício?
Nesse problema temos um sistema com cabos e uma foça que aponta para cima e nosso objetivo é encontrar as trações dos cabos e a força se o cabo tem tração de .
Parece complicado?
Para resolver esse problema basta aplicar as equações de conservação de forças:
Saca só!
Passo 2
No eixo temos:
No eixo , temos:
E para o eixo , temos:
Juntando as três equações de equilíbrio...
Tranquilo até aqui?
Passo 3
Foi dito no enunciado que , ou seja:
Resolvendo esse sistema, vamos chegar em:
E substituindo na última equação, vamos obter:
É isso! O que achou? Responde Aí!