Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 9.Problemas - Ex. 82

Determine a profundidade h do furo de 100   m m de diâmetro feito na base do cone de modo que o centro de massa do sólido resultante esteja localizado em z -   =   115   m m . O material tem densidade de 8   M g / m 3 .

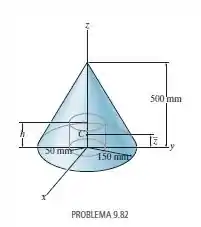
Passo 1

Oi tudo bem? Vamos resolver este exercício.

Queremos a massa e a localização ( x - ,   y - ,   z - ) do centro de massa G desta placa composta de aço e latão.

Para o cálculo da massa, temos que:

m = ρ ⋅ V

O volume da placa é igual ao produto do comprimento, largura e espessura do elemento.

Vamos dividir o elemento da seguinte maneira:

A massa da parte 1 será:

m 1 = 7,85   M g / m 3 1000 k g M g ⋅ 150 ⋅ 10 - 3   m 225 ⋅ 10 - 3   m 30 ⋅ 10 - 3   m

m 1 = 7,85 ⋅ 10 3 ⋅ 0,15 ⋅ 0,225 ⋅ 0,3

m 1 = 7,95   k g

A massa da parte 2 será:

m 2 = 7,85   M g / m 3 1000 k g M g ⋅ 1 2 150 ⋅ 10 - 3   m 225 ⋅ 10 - 3   m 30 ⋅ 10 - 3   m

m 2 = 7,85 ⋅ 10 3 ⋅ 1 2 ⋅ 0,15 ⋅ 0,225 ⋅ 0,3

m 2 = 3,975   k g

A massa da parte 3 será:

m 3 = 8,74   M g / m 3 1000 k g M g ⋅ 1 2 150 ⋅ 10 - 3   m 225 ⋅ 10 - 3   m 30 ⋅ 10 - 3   m

m 3 = 8,74 ⋅ 10 3 ⋅ 1 2 ⋅ 0,15 ⋅ 0,225 ⋅ 0,3

m 3 = 4,425   k g

Passo 2

A localização do centroide do elemento 1 com relação a x será:

x 1 = 0,150 2

x 1 = 0,075   m

A localização do centroide do elemento 2 com relação a x será:

x 2 = 0,15 3 + 0,15

x 2 = 0,2   m

A localização do centroide do elemento 3 com relação a x será:

x 3 = 0,15 2 3 + 0,15

x 1 = 0,25   m

Passo 3

A localização do centroide do elemento 1 com relação a z será:

z 1 = 0,225 2

z 1 = 0,1125   m

A localização do centroide do elemento 2 com relação a z será:

z 2 = 2 3 ( 0,225 )

z 2 = 0,15   m

A localização do centroide do elemento 3 com relação a x será:

z 3 = 1 3 0,225

z 1 = 0,075   m

Passo 4

De posse destes dados podemos encontrar o centroide do elemento inteiro, bem como sua massa total.

Temos que:

M = ∑ m i

Logo:

M = m 1 + m 2 + m 3

M = 7,95 + 3,975 + 4,425

M = 16,35   k g

O centro de massa da placa composta em torno de x será:

x - = ∑ x i m i ∑ m i

x - = 0,075 7,95 + 0,2 3,975 + 0,25 4,425 16,35

x - = 0,15275   m

O centro de massa da placa composta em torno de y será:

y - = - 1 2 30 ⋅ 10 - 3

y - = - 0,015   m

O centro de massa da placa composta em torno de z será:

z - = ∑ z i m i ∑ m i

z - = 0,1125 7,95 + 0,15 3,975 + 0,075 4,425 16,35

z - = 0,11145   m

Resposta

x - = 0,15275   m

y - = - 0,015   m

z - = 0,11145   m

M = 16,35   k g

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma correia circular em “ V ” possui raio interno de 600m m e uma seção transversal conformemostra a figura. Determine o volume do material exigido para fabricar a correia.
O que significa homogeneidade dimensional de uma equação física? Por que se faznecessária essa homogeneidade?
Por que os objetos ficam ligeiramente mais pesados no Pólo Norte do que no Equador, como também mais pesados durante a noite do que durante o dia?
Por que adotar o conceito de algarismos significativos ao resolver problemas de engenharia? Como efetuar arredondamentos de resultados numéricos desses problemas?
Como são definidos o ângulo plano e o ângulo sólido? Quais são as respectivas unidades e símbolos no SI?