Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 17.Problemas - Ex. 108

Uma esfera uniforme de raio r rola para baixo sobre o plano inclinado mostrado na figura sem deslizar. Ela atinge uma superfície horizontal e, após deslizar por um momento, começa a rolar novamente. Considerando que a esfera não quica ao atingir a superfície horizontal, determine sua velocidade angular e a velocidade de seu centro de massa após recomeçar a rolar.

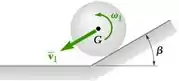
Passo 1

E aí galerinha tudo belezinha? O enunciado pede que a gente determine sua velocidade angular e a velocidade de seu centro de massa após recomeçar a rolar.

Temos então que o momento de inércia. De uma esfera sólida é dada por:

I - = 2 5 m r 2

Passo 2

Antes do impacto (rolando) a velocidade é dada por:

v 1 = r ω 1

Depois que o escorregamento parou.

v - 2 = r ω 2

Passo 3

Momentos sobre C é dada pela relação das inércias e velocidade :D

I - ω 1 + m v 1 r cos ⁡ β + 0 = I - ω 2 + m v - 2 r

I - ω 1 + m r 2 ω 1 cos ⁡ β = I - ω 2 + m r 2 ω 2

ω 2 = I - + m r 2 cos ⁡ β I - + m r 2 ω 1 = 2 5 m r 2 + m r 2 cos ⁡ β 2 5 m r 2 + m r 2 ω 1

v - 2 = r ω 2 = 2 + 5 cos ⁡ β 7 r ω 1

Resposta

ω 2 = 1 7 2 + 5 cos ⁡ β ω 1  

v - 2 = 1 7 2 + 5 cos ⁡ β v - 1 ←

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas hastes, cada uma com massa m e comprimento L, são soldadas para formar o conjunto mostrado. Determine (a) a distância b para a qual a frequência de pequenas oscilações da montagem é máxima, (b) a
19.114. À medida que a velocidade de rotação de um motor de 100 kg apoiado por molas é aumentada, a amplitude da vibração, causada pelo desbalanceamento do seu rotor de 15 kg, primeiro aumenta e depoi
19.117. Um motor de 100 kg é parafusado a uma viga horizontal leve. O desbalanceamento do seu rotor é equivalente a uma massa de 60 g localizada a 100 mm do eixo de rotação. Sabendo que a ressonância
19.120. Um certo acelerômetro consiste essencialmente de uma caixa contendo um sistema massa-mola com uma frequência natural conhecida de 2.200 Hz. A caixa é rigidamente ligada a uma superfície que es
19.115. Um motor de 200 kg é suportado por molas que têm um constante total de 240 kN/m. O desbalanceamento do rotor é equivalente a uma massa de 30 g localizada a 200 mm do eixo de rotação. Determine