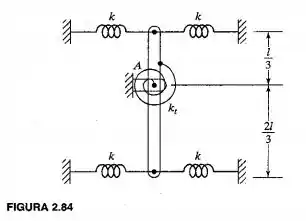
Uma haste delgada uniforme de massa e comprimento é articulada no ponto A e está ligada a quatro molas lineares e uma mola torcional, como mostra a Figura 2.84. Determine a a frequência natural do sistema se , , e.
Passo 1
Queremos a frequência natural do sistema dado na figura do enunciado.
Vamos calcular o momento de inércia de massa da haste delgada sobre o seu centro de gravidade :
O momento de inércia de massa da haste, no ponto será:
Onde é a distância entre o centro de gravidade e o ponto .
O centro de gravidade da haste fica no seu meio: .
A distância será:
Portanto:
Passo 2
Aplicando o principio do momento angular sobre o ponto , obtemos a seguinte equação de movimento para o sistema:
Onde, indica o peso da haste e é a aceleração angular da haste.
Desenvolvendo a equação, temos que:
Sabemos que a equação de movimento para o sistema dado pode ser modelada como:
Portanto, temos que:
Substituindo os dados, temos que: