Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 142
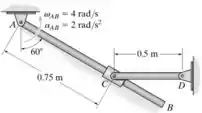
No instante mostrado, a barra AB tem uma velocidade angular e uma aceleração angular . Determine a velocidade angular e a aceleração angular da barra CD nesse instante. O anel em C está conectado por pino a CD e desliza livremente ao longo de AB.
Passo 1
A origem dos eixos coordenados, seja ele o referencial ou o fixo, iremos considerar como tendo sua origem no ponto A, como a mostra a figura abaixo.
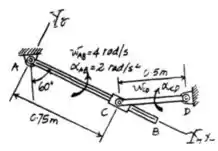
Além disso, vamos escrever o que o enunciado nos fornece:
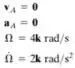
Iremos escrever também o movimento relativo do ponto C:
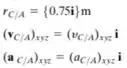
Passo 2
Calcularemos, agora, as equações da velocidade relativa e da aceleração relativa.
A velocidade de pode ser calculada a partir de , com isso,
Passo 3
A aceleração, , pode ser calculada pela fórmula abaixo:
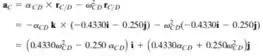
Passo 4
Vamos calcular .
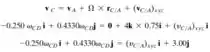
Igualando as componentes i e j, teremos:
Passo 5
Agora que encontramos o valor de , vamos substituir esse valor na fórmula da aceleração, Passo 3, para que a gente encontre o valor de .
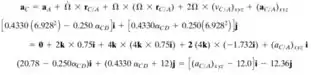
Igualando as componentes i e j, teremos:
