Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.7 - Ex. 164

O mecanismo é constituído por duas barras esbeltas e se move no plano horizontal sob influência da força P . A barra O C tem uma massa m e a barra A C tem massa 2 m . O bloco deslizante em B tem massa desprezível. Sem desmembrar o sistema, determine a aceleração angular inicial α das barras quando P é aplicado em A , com as barras inicialmente em repouso. (Sugestão: Substitua P pelo seu sistema força-momento equivalente).

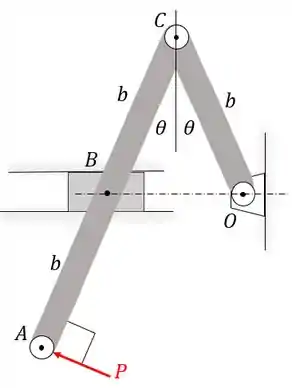
Passo 1

O enunciado nos dá as seguintes informações:

Massa da barra O C : m

Massa da barra A C : 2 m

Devemos determinar a aceleração angular inicial α das barras quando P é aplicada em A , com as barras inicialmente em repouso.

Além disso, sabemos que as barras estão inicialmente em repouso.

Passo 2

Vamos assumir que a força P seja deslocada para o ponto B , conforme o diagrama abaixo:

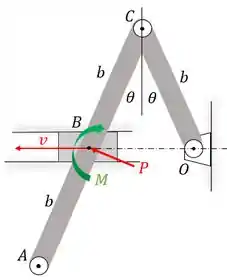
Onde o momento M será M = P b .

Agora vamos aplicar a Equação de Trabalho-Energia para movimento infinitesimais

d U = d T + d V

Onde

d U = P cos ⁡ θ d 2 b sen ⁡ θ + P b d θ

d U = P b 2 cos 2 ⁡ θ + 1 d θ

d T = d T A C + d T O C

d V = 0

O valor de d V é igual a zero pois nao há variação na energia potencial gravitacional total e a energia potencial elástica não é aplicável neste problema.

Já sabemos o valor de d U , portante devemos encontrar o valor de d T .

Passo 3

Temos que

d T A C = d 1 2 2 m v 2 + 1 2 I - ω 2

d T A C = 2 m v d v + I - ω d ω

Sabemos que

v = d x d t

E que

a = d v d t

Logo,

2 m v d v = 2 m d x d t a d t = 2 m a d x

Além disso, sabemos que

ω = d θ d t = θ ˙

E que

α = d ω d t = θ ¨

Logo,

I - ω d ω = I - d θ d t α d t = I - α d θ

Portanto, obtemos

d T A C = 2 m a d x + I - α d θ

Onde

x = 2 b sen ⁡ θ

v = 2 b θ ˙ cos ⁡ θ

a = 2 b θ ¨ cos ⁡ θ - θ ˙ 2 sen ⁡ θ = 2 b θ ¨ cos ⁡ θ

Por fim, temos que

d T A C = 2 m 2 b θ ¨ cos ⁡ θ d 2 b sen ⁡ θ + 1 12 2 m 2 b 2 θ ¨ d θ

d T A C = 2 m b 2 4 cos 2 ⁡ θ + 1 3 θ ¨ d θ

Passo 4

Agora vamos encontrar d T O C .

Temos que

d T O C = d 1 2 I O - ω 2

d T O C = I O ω d ω = I O α d θ

d T O C = I O d θ d t α d t = I O α d θ = 1 12 m b 2 θ ¨ d θ

d T O C = 1 3 m b 2 θ ¨ d θ

Passo 5

Substituindo os valores encontrados acima na Equação d U = d T + d V , obtemos

P b 2 cos 2 ⁡ θ + 1 d θ = 2 m b 2 4 cos 2 ⁡ θ + 1 3 θ ¨ d θ + 1 3 m b 2 θ ¨ d θ

P b 2 cos 2 ⁡ θ + 1 d θ = m b 2 8 cos 2 ⁡ θ + 1 θ ¨ d θ

Sabemos que α = θ ¨ , logo, colocando θ ¨ em evidência, obtemos

  α = θ ¨ = P b 2 cos 2 ⁡ θ + 1 m b 2 8 cos 2 ⁡ θ + 1

Resposta

α = P b 2 cos 2 ⁡ θ + 1 m b 2 8 cos 2 ⁡ θ + 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A roda e a bobina a ela fixada têm uma massa combinada de 25 kg e raio de giração em relação a seu centro k A = 150m m . Se a polia B fixada ao motor é submetida a um torque M = 60 2 - e - 0,1 θN . m
Resolva o Problema 18.12, se o coeficiente de atrito cinético entre a bobina e o plano em A for μ k = 0,2 .
Se o sistema é solto do repouso, determine a velocidade dos cilindros de 20 kg, A e B, após A ter se deslocado para baixo uma distância de 2 m. A polia diferencial tem massa de 15 kg e raio de giração
A tampa da caixa de 6 kg é mantida em equilíbrio pela mola torsional em θ = 60 ° . Se a tampa é forçada a fechar-se, θ = 0 ° , e em seguida é liberada, determine sua velocidade angular no instante em
A roda e a bobina a ela fixada têm uma massa combinada de 25 kg e raio de giração em relação a seu centro k A = 150m m . Se a polia B, que está fixada ao motor, for sujeita a um torque M = 75N . m , d