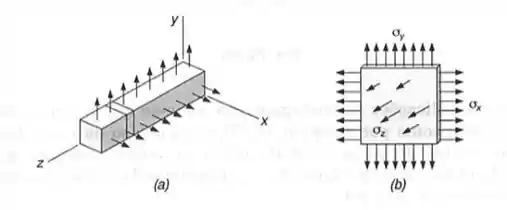
Em muitas situações físicas, os vínculos impedem que as deformações especificas ocorram em uma dada direção, por exemplo, , para o caso mostrado, onde o movimento longitudinal de qualquer ponto do prisma não é permitido. Assim, seções planas perpendiculares ao eixo longitudinal permanecem planas e separadas com afastamento constante. Mostre que, para esta situação, na qual é conhecida o estado plano de deformação, podemos expressar :

Esse exercício é demonstrativo, logo, precisamos dar uma certa atenção para o nosso problema, logo, para fazermos isso, precisamos ter em mãos as nossas leis generalizadas de Hooke, e a partir delas resolver o nosso problema, com isso teremos que:

E pelo nosso enunciado definimos que conhecemos o estado plano de deformações, ou seja, sabemos os valores de e e sabemos que o valor de vale zero. Começando por , teremos que:

Como já sabemos que a deformação é zero, iremos substituir isso e definir o valor da tensão na direção Z.

Substituindo teremos que:

Agora vamos substituir nas nossas fórmulas principais para definirmos as deformações em função das tensões em x e y, sendo assim teremos que:

E a deformação na direção y será feito da seguinte maneira: