Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 20.Problemas - Ex. 38

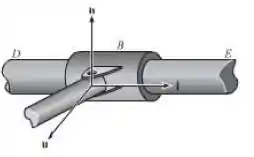
Resolva o problema 20.37 se a conexão em B consistir de um pino, como mostrado na figura, em vez de uma junta esférica. Dica: a restrição permite a rotação da barra tanto em torno da barra D E (direção j ) quanto em torno do eixo do pino (direção n ). Visto que não há uma componente rotacional na direção u , ou seja, perpendicular a n   e   j onde u = j × n , uma equação adicional para a solução pode ser obitida de ω ⋅ u = 0 . O vetor n está na mesma direção que r B / C × r D / C .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

O enunciado nos pede a velocidade do anel B .

Vamos às analises:

ω = ω x i + ω y j + ω z k

v B = - v B j   m / s

r B / C = - 0,2 i + 0,6 j + 0,3 k

v B = v C + ω B C × r B / C

- v B j = 1 i + i j k ω x ω y ω z 1,25 2,165 0

1 - ω y - 0,6 ω z = 0

0,3 ω x + 0,2   ω z = v B

0,6 ω x + 0,2 ω y = 0

Temos que:

r B / C = - 0,2 i + 0,6 j + 0,3 k

r D / C = - 0,2 i + 0,3 k

r B / C × r D / C = 0,18 i + 0 , 12 k   m 2

Sabemos que:

n = 0,18 i + 0,12 k 0,18 2 + 0,12 2

n = 0,8321 i + 0 , 5547 k

u = j × n = j × 0,8321 i + 0,5547 k = 0,5547 i - 0,8321 k

Logo:

0,5547 ω x - 0,8321 ω z = 0

Resolvendo, temos:

ω x = 0,769   r a d / s

ω y = - 2,31   r a d / s  

ω z = 0,513   r a d / s

v B = 0,333   m / s

Logo:

ω B C = 0 , 769 i - 2 , 31 j + 0,513 k

v B = - 0,333 j   m / s

Resposta

ω B C = 0,769 i - 2,31 j + 0,513 k

v B = - 0,333 j   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No instante θ = 30 ° , o corpo do satélite está girando com uma velocidade angular ω 1 = 29r a d / s , e tem uma aceleração angular ω ˙ 1 = 5r a d / s 2 . Simultaneamente, os painéis solares giram com
Quando a barra AB está na posição mostrada, o anel A se desloca com uma velocidade v A = { 3 i } m/s e aceleração a A = { 0,5 i } m/s2, determine a aceleração do anel B nesse instante. Suponha que a v
Se o anel A se desloca com uma velocidade constante v A = { 3 i } m / s , determine a velocidade do anel B quando a barra AB está na posição mostrada. Suponha que a velocidade angular de AB é perpendi
A manivela AO gira no sentido horário com uma velocidade angular constante de 10 rad/s dentro de um arco limitado de seu movimento. Para a posição θ = 30 ° determine a velocidade angular da barra ranh
O ônibus espacial A está em uma órbita circular equatorial de 240 km de altitude e está se movendo de oeste para leste. Determine a velocidade e a aceleração que ele parece ter para um observador B fi