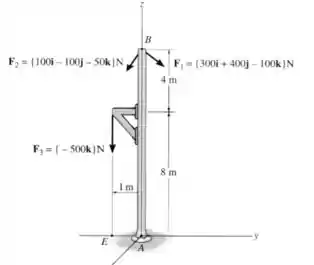
Substitua o sistema de forças por uma força e um momento equivalentes no ponto .
Passo 1
Vamos começar encontrando a força resultante que age sobre o sistema. Para isso precisamos fazer a soma vetorial das três forças que foram dadas no enunciado:
Passo 2
Agora precisamos calcular o momento resultante dessas forças em relação ao ponto :
O primeiro passo é escrever cada um desses vetores de posição:
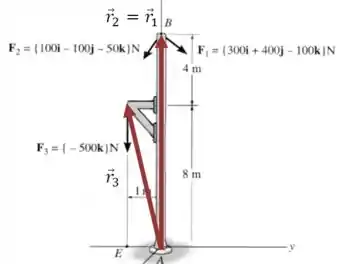
Então vamos escrever cada um daqueles produtos vetoriais como um determinante:
Passo 3
Agora vamos resolver cada um desses termos:
Então:
Resposta
O sistema pode ser substituído por uma força e por um momento .