85- A barra é apoiada por uma junta esférica em e por um cabo em . Determine os componentes de reação nesses apoios, sabendo que a barra está sujeita a uma força vertical de , como é mostrado na figura.
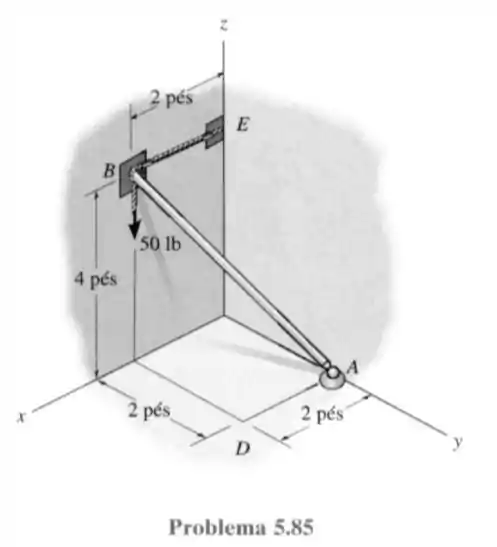
Passo 1
Vamos desenhar o sistema de forças na barra.
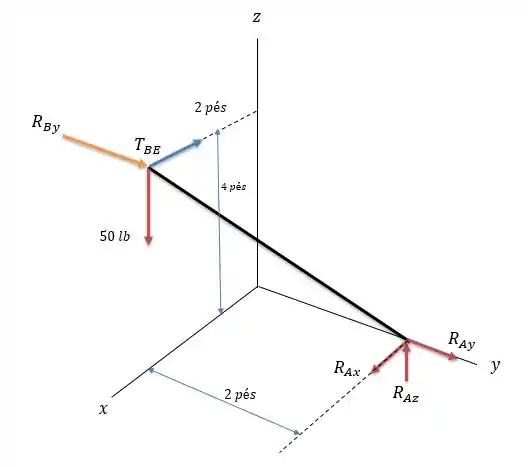
Onde a junta esférica oferece reações de força em todos os sentidos.
Passo 2
Vamos analisar as forças primeiro:
Fazendo a somatória das forças em nós teremos:
Agora o somatório das forças em :
E o somatório das forças em
Passo 3
Agora podemos ir para os momentos:
Vamos analisar os momentos que gera em .
A força de gera momento em e em
A somatória dos momentos em nos dá:
Do passo conseguimos dizer que:
Agora a somatória dos momentos em :
Do passo podemos dizer:
A somatória dos momentos em nos confirmaria a igualdade entre e .