Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas - Ex. 74
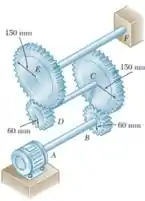
Três eixos e quatro engrenagens são utilizados para formar um trem de engrenagens que transmite a potência do motor em A para a máquina ferramenta em F. (os mancais para os eixos são omitidos no esquema). O diâmetro de cada eixo são os que seguem: . Sabendo que a frequência do motor é de 24 Hz e que a tensão de cisalhamento admissível para cada eixo é de 75 MPa, determine a máxima potência que pode ser transmitida.
Passo 1
E ai gurizada tudo belezinha? O exercício pede que a gente, determine a máxima potência que pode ser transmitida. Considerando a tensão:
Vamos para o eixo AB:
O raio é :
A partir da equação da tensão podemos determinar o torque isolando T
A frequência é e a potência pode ser determinada como apresentada abaixo, vem comigo :D
Passo 2
Agora, vamos para o eixo CD:
O raio é:
A partir da equação da tensão podemos determinar o torque isolando T
Agora temos que determinar a frequência e a potência pode ser determinada como apresentada abaixo, vem comigo :D
Passo 3
E por fim, para o eixo EF:
O raio é:
A partir da equação da tensão podemos determinar o torque isolando T
Agora temos que determinar a frequência e a potência pode ser determinada como apresentada abaixo, vem comigo :D
Para nossa resposta temos que escolher o menor valor permitido:
Resposta
Então gurizada, a máxima potência de transmissão será o menor valor encontrado, que é: .