Três molas e uma massa estão ligadas a uma barra rígida sem peso PQ, como mostra a figura. Determine a frequência natural de vibração do sistema.
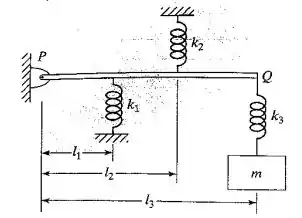
Passo 1
Vamos lá resolver mais essa. Vamos utilizar a conservação de energia para calcular a constante elástica equivalente do conjunto formado pela mola 1, mola 2 e a barra PQ. Assumindo que este sistema tem deslocamentos angulares pequenos, podemos relacionar a energia potencial elástica do sistema como:
Passo 2
Agora, vamos supor que o conjunto do passo anterior seja uma mola ligada em série com a mola três no ponto Q. Com isso, podemos calcular a constante elástica equivalente para um sistema como um todo:
Passo 3
A frequência natural pode ser calculada como: