Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 11.Problemas - Ex. 30

A viga com avanço foi construída com duas peças de madeira de 50 mm por 100 mm escoradas como mostra a figura. Se a tensão de flexão admissível for σ a d m = 4,2   M P a , determine a maior carga P que pode ser aplicada. Calcule também o espaçamento máximo associado, s, entre os pregos ao longo da seção AC da viga se cada um deles puder resistir a uma força de cisalhamento de 4   k N . Considere que a viga está unida por pinos em A, B e D. Despreza a força axial desenvolvida na viga ao longo de DA

Passo 1

Vamos fazer o diagrama de corpo livre desta viga

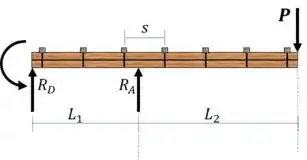
É uma viga hiperestática, e não podemos determinar as reações de apoio. Mas perceba que devido a forma do carregamento, o cisalhamento máximo e o momento máximo serão no ponto A.

V m a x = P

M m a x = P ⋅ L 2

Passo 2

Agora, vamos calcular o momento de inércia da seção:

I = 100 ⋅ 100 3 / 12

I = 1 12 10 8   m m 4

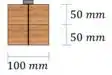
E o momento estático:

Q = 50 ⋅ 100 ⋅ 25

Q = 125000   m m 3

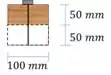
Passo 3

Vamos aplicar a equação da flexão para determinar a força

σ a d m = c ⋅ M m a x I  

σ a d m = c ⋅ P ⋅ L 2 I  

Isolando o P :

P = σ a d m I c L 2

P = 4,2   M P a ⋅ 1 12 10 8 m m 4 50   m m ⋅ 900   m m

P = 777,78   N

Passo 4

Agora vamos igualar o fluxo de cisalhamento sobre o prego com o fluxo de cisalhamento sobre uma das tábuas:

F p r e g o s = V Q I

F p r e g o s = P Q I

s = F p r e g o I P Q

s = 4 k N ⋅ 1 12 10 8   m m 4 777,78   N ⋅ 125000   m m 3

s = 342,85   m m

Resposta

P = 777,78   N

s = 342,85   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sabendo-se que o tubo estrutural mostrado tem uma espessura da parede uniforme de 8m m , determinar a tensão de cisalhamento em cada um dos dois pontos indicados.
Para a viga extrudada, com a seção transversal mostrada, determinar a localização do centro de cisalhamento O.
Determinar a localização do centro de cisalhamento O, de uma viga de parede fina de espessura uniforme e com a seção transversal mostrada.
Resolver o Prob 5.95 , considerando que a força de 65k N aplicada no ponto A atua verticalmente para baixo.
Sabendo-se que o tubo estrutural mostrado tem uma espessura da parede uniforme de 6m m , determinar a tensão de cisalhamento em cada um dos três pontos indicados.