Exercícios de Fórmula do Cisalhamento - Lista de Exercícios Resolvida
Questão 1
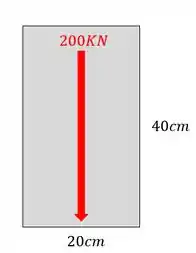
Abaixo é dada uma seção retangular de altura 40cm e base 20 cm. Sabendo que a seção somente suporta uma tensão cisalhante de no máximo 500Kpa, determine a que altura ocorreria a tensão cisalhante imediatamente anterior ao rompimento da mesma. Vale ressaltar que a peça está sofrendo a ação de um cortante de 200KN na direção mostrada.
Questão 2
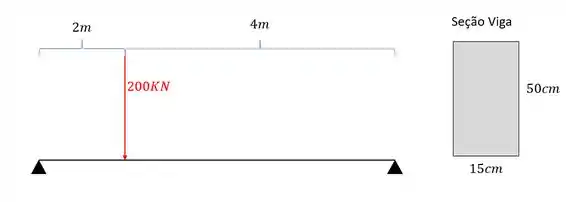
Abaixo é dado uma viga sujeita as cargas mostradas. Com base nos seus conhecimentos, determine a tensão cisalhante máxima que afeta a viga mostrada abaixo.
Questão 3
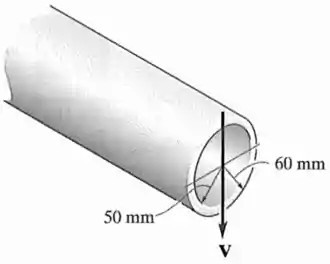
Se o tubo estiver sujeito a um cisalhamento , determine a tensão de cisalhamento máxima nele.
Dicas do Expert: Existem alguns conhecimentos adicionais importantes para resolver exercícios com uma seção circular como este.
São eles:
1. A tensão de cisalhamento máxima em seções transversais circulares (vazadas ou não) ocorre na linha neutra da seção;
2. Para o cálculo da posição da linha neutra, do momento de inércia da área e do momento estático, você pode considerar furos como elementos de área negativa e momento de inércia da área negativo;
& 3. A centroide de um semicírculo de raio fica a uma distância da base do semicírculo.
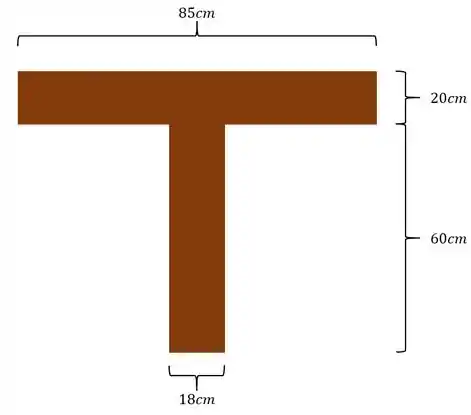
Ver solução completaQuestão 4
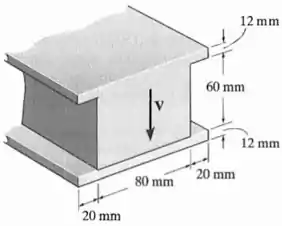
Faça um gráfico da intensidade da tensão de cisalhamento distribuída na seção transversal da escora se ela for submetida a uma força de cisalhamento .
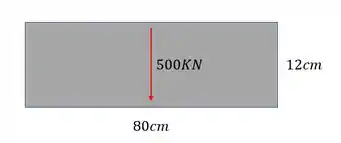
Questão 5
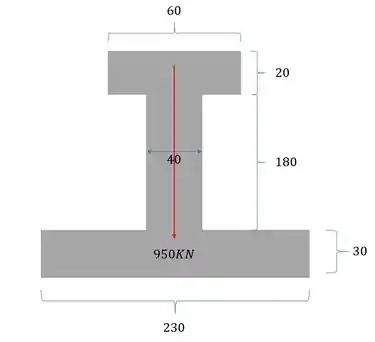
Determine a tensão cisalhante máxima na seção sujeita ao esforço cortante mostrado abaixo. Todas as medidas estão em cm.
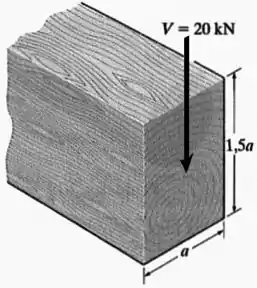
Questão 7
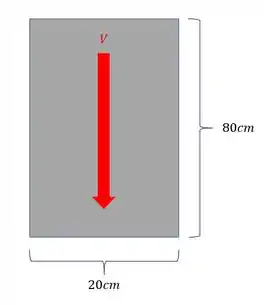
Uma viga de seção retangular com as dimensões mostradas na figura, foi submetida a um carregamento cortante de intensidade . Sabendo que a tensão cisalhante admissível máxima suportada por essa viga é , determine o valor do cortante máximo que podemos aplicar sem que haja rompimento da peça.
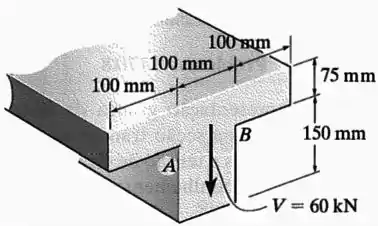
Questão 8
Se a viga for submetida a um cisalhamento vertical , determine a tensão de cisalhamento máxima na viga. Calcule também o salto da tensão de cisalhamento na junção aba-alma . Trace um rascunho da variação da intensidade da tensão de cisalhamento em toda a seção transversal.