A velocidade de um corredor aumenta regularmente durante os três primeiros segundos de uma corrida. Sua velocidade em intervalos de meio segundo é dada em uma tabela. Encontra as estimativas superior e inferior para a distância que ele percorreu durante esses 3 segundos.

Passo 1
Faaala, meus queridos! Tudo bem com vocês?
Essa questão dá uma tabela com os valores da velocidade de um corredor ao longo do tempo. Os valores dados são esses aqui:

O enunciado pede pra usarmos esses valores pra fazermos uma estimativa superior e uma inferior da distância percorrida pelo corredor.
Vamos ver como fazemos isso juntos!
Passo 2
Pra resolvermos essa questão precisamos lembrar que quando temos um gráfico de velocidade por tempo, podemos calcular a distância percorrida pela área do gráfico.
A maneira mais prática de estimarmos áreas e aproximando pela soma das áreas de vários retângulos. E é justamente isso que vamos fazer! Existem duas relações pra esse cálculo:
A diferença entre essas relações é que na primeira, os retângulos são ajustados no gráfico pelas extremidades esquerdas e na segunda, os retângulos são ajustados no gráfico pela extremidade direita. Se isso não ficou tão claro ainda, fica tranquilo(a) que vamos ver um exemplo de como isso funciona.
Como essa questão pede pra calcularmos uma estimativa superior (maior do que o valor real) e uma estimativa inferior (menor do que o valor real), já imaginamos que vamos precisar das duas relações acima.
Vem comigo!
Passo 3
Vamos nessa! Essa questão pede pra usarmos os valores tabelados da velocidade em função do tempo pra estimarmos a distância percorrida nesse intervalo de tempo.
Pra isso, precisamos lembrar que a distância percorrida pode ser calculada pela área abaixo do gráfico da velocidade pelo tempo! É justamente o valor dessa área que vamos tentar estimar.
A questão pede pra encontrarmos a estimativa superior e inferior pra essa distância. O que ele quer dizer com isso?
Basicamente, nós podemos estimar a área embaixo de uma curva usando retângulos ajustados à esquerda ou a direita na função. Olha aqui um exemplo:
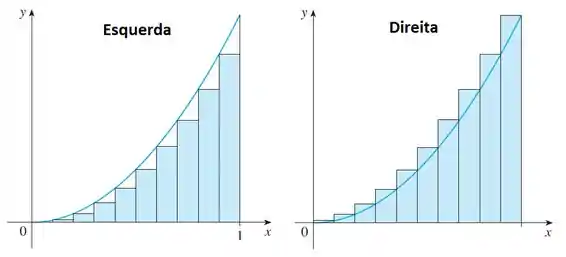
Essas áreas são dadas pelas expressões:
, onde é a largura dos retângulos e é a quantidade de retângulos. Os valores até são pontos intermediários onde marcamos os nossos retângulos. Isso significa que se tivermos pontos, temos retângulos.
Não precisamos esboçar o gráfico específico fazer a questão. Os valores na tabela vão bastar pra gente.
Passo 4
Vamos dar uma olhada nos valores mais uma vez:

Se liga que a função velocidade é crescente! Isso significa que a estimativa superior da área vai ser dada usando as extremidades direitas e a estimativa inferior da área vai ser dada usando as extremidades esquerdas! Assim como na figura exemplo ali em cima. Ou seja, temos o seguinte:
Como temos pontos, vamos usar retângulos pra calcular as nossas áreas. Vamos começar com a estimativa superior:
Colocando em termos do tempo e da velocidade, temos:
Substituindo os valores da tabela, fica assim:
Agora é só terminar a nossa conta:
Vamos calcular agora a estimativa inferior
Passo 5
Calculando a estimativa inferior, temos:
Colocando novamente em termos do tempo e da velocidade, temos:
Substituindo os valores da tabela, temos:
Boooa! Conseguimos terminar!