Intervalo de Confiança

Estudando probabilidade e estatística? Precisando aprender sobre Intervalo de Confiança? Então você está no lugar certo.

Vamos introduzir essa ideia de intervalo de confiança aqui. Partiu?

Uma das coisas que fazemos em estatística é estimar um parâmetro qualquer de uma população a partir de um único valor amostral, porém esse processo é muito incerto, não temos como saber se o valor que estimamos está realmente perto do valor real ou não, é complicado estimar corretamente o valor de um parâmetro.

Parece um pouco mais razoável a gente determinar um intervalo, no qual o valor real do parâmetro estaria contido. E é esse intervalo que chamamos de intervalo de confiança.

Para determinar esse intervalo nós vamos calcular um limite inferiror e um limite superior e o nosso parâmetro qualquer, , poderá estar entre esses limites:

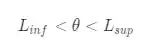
E para calcularmos esses limites vamos definir um nível de confiança. Por exemplo, eu quero achar um intervalo de confiança em que eu tenha de confiança de que meu parâmetro esteja contido nesse intervalo, sacou? Em outras palavras, temos que nos perguntar o seguinte: Qual é o valor de e para que a probabilidade do meu parâmetro estar entre esses limites seja de ?

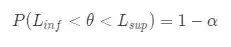
Onde:

• será nosso intervalo de confiança, e;
• é o nosso nível de confiança

Obs.: Para não ficarmos escrevendo Intervalo de Confiança toda hora vamos usar a sigla IC, beleza?

Normalmente, nós temos três casos para calcular intervalo de confiança, são eles:

• IC para média populacional, com conhecido;
• IC para média populacional, com desconhecido, e;
• IC para proporção amostral

Por exemplo, o IC para a média populacional, que segue uma distribuição normal, com conhecido é dado por:

Onde:

• é a média amostral;
• é o tamanho da amostra;
• é o desvio padrão da amostral;
• é valor que encontramos na tabela normal padrão, que tem probabilidade igual a .

QUE??? Como você encontrou essa expressão aí para os limites do intervalo??

Calma calma, sem desespero hahaha, eu coloquei a expressão logo aí pra você ficar curioso mesmo hahaha. Quer entender como chega nisso? Então assiste esse video aqui:

Agora que você já entendeu a ideia do intervalo de confiança e como encontrá-lo para a média populacional com o conhecido, pode continuar seu estudo e aprender os demais casos não é mesmo? Então confere logo aqui em seguida 👇🏽 o Raio-X que fizemos com todo o conteúdo sobre intervalo de confiança, bem organizadinho para você estudar. 😉