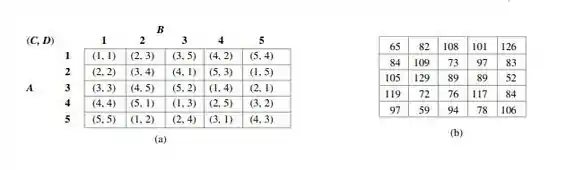
Analogamente ao quadrado latino, um modelo em quadrado greco-latino pode ser usado quando existe a suspeita de que três fatores externos podem influenciar a variável de resposta e os quatro fatores (os três externos e o de interesse) têm o mesmo número de níveis. No quadrado latino, cada nível do fator de interesse (C) aparece uma vez em cada linha (com cada nível de ) e uma vez em cada coluna (com cada nível de ). No quadrado greco-latino, cada nível do fator aparece uma vez em cada linha, em cada coluna e também com cada nível do terceiro fator externo . Alternativamente, esse modelo pode ser usado quando os quatro fatores têm o mesmo grau de interesse, o ficientes apenas para observações. Um quadrado 5 é ilustrado em (a), no qual em cada célula representa o -ésimo nível de e o -ésimo de . Em (b), apresentamos os dados da perda de peso em barras de silício usadas no material semicondutor como uma função do volume de solução ácida , cor do ácido nítrico na solução ácida , tamanho das barras e tempo dentro da solução ácida (D) (com base em "Applications of Analytic Techniques to the Semiconductor Industry", Fourteenth Midwest Quality Control Conference, 1959).
Considere a perda de peso observada quando o fator está no nível está no nível está no nível e está no nível . Supondo que não há nenhuma interação entre os fatores, a soma de quadrados total SQT (com gi) pode ser dividida em SQA, SQB, SQC, SQD e SQE. Apresente expressōes para essas somas de quadrados, incluindo fórmulas de cálculo, obtenha a uma das hipóteses dos quatro efeitos principais, usando
Passo 1
E aí pessoal partiu para mais uma questão de probabilidade? Abaixo começaremos trazendo algumas informações do enunciado:
Considere a perda de peso observada quando o fator está no nível está no nível está no nível e está no nível . Supondo que não há nenhuma interação entre os fatores, a soma de quadrados total SQT (com gi) pode ser dividida em SQA, SQB, SQC, SQD e SQE. Apresente expressōes para essas somas de quadrados, incluindo fórmulas de cálculo, obtenha a uma das hipóteses dos quatro efeitos principais, usando .
, com expressões semelhantes para SSB, SSC e SSD, cada um tendo . with , deixando df para erro.
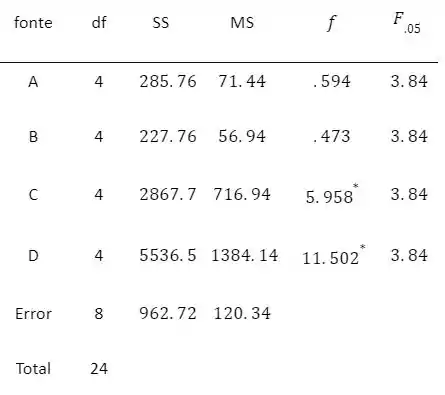
e não podem ser rejeitados, enquanto e são rejeitados.
Resposta
e não podem ser rejeitados, enquanto e são rejeitados.
Espero que tenham aprendido com essa questão, até a próxima !