Calculando e interpretando escores-z. Nos exercícios 39 e 40, (a) encontre os escores-z que correspondem a cada valor e (b) determine se algum dos valores é incomum.
Pontuação do SAT
O SAT é um exame usado por faculdades e universidades dos Estados Unidos para avaliar candidatos à graduação. As pontuações do exame são normalmente distribuídas. Em um ano recente, a pontuação média do teste foi de 1.498 e o desvio padrão foi de 316. As pontuações dos testes de quatro estudantes escolhidos aleatoriamente são 1.920, 1.240, 2.200 e 1.390. (Fonte: College Board.)
Passo 1
Fala aí galera, bora resolver o nosso exercício? Vamos lá, começando pela (a).
Para começar, vamos destacar a média, o desvio padrão e as pontuações dos quatro estudantes:
1.920, 1.240, 2.200 e 1.390
Beleza, com as informações acima, vamos calcular:
Se a gente for organizar numa tabelinha, teremos:
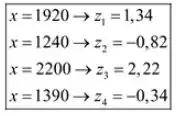
Passo 2
Por fim, vamos para a (b).
Vamos pegar aqui os valores:
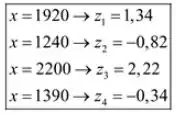
Antes de tudo, importante destacar aqui que um valor é incomum quando os valores das pontuações diferem de dois ou mais desvios padrão do valor da média amostral.
Assim podemos concluir que para o terceiro estudante, que tirou 2200 pontos e o escore-z é de 2,22, notamos que este valor é incomum pois possui mais que dois desvios padrão de diferença da média.