O conjunto de dados representa o tempo (em minutos) gasto assistindo a vídeos on-line a cada dia para uma amostra aleatória de 30 estudantes universitários. Suponha que o desvio padrão populacional é de 2,4 minutos. (Adaptado de: The Council for Research Excellence.)

(a) Calcule a estimativa pontual da média populacional.
(b) Calcule a margem de erro para um nível de confiança de 95%.
(c) Construa um intervalo de confiança de 95% para a média populacional. Interprete os resultados.
Passo 1
Olá galera, tudo bem? Vem resolver esse problema comigo.
Uma estimativa pontual é um valor único estimado para um parâmetro populacional. A média amostral () é um estimador não tendencioso para a média populacional (). Onde:
Então no item (a) iremos utilizar a média amostral para encontrarmos a estimativa pontual da média populacional.
Temos que:
Passo 2
A margem de erro é a maior distância possível entre a estimativa pontual e o valor do parâmetro que ela está estimando, dado um determinado nível de confiança . Para uma média populacional (), em que o desvio padrão populacional () é conhecido:
Isso é valido para as condições:
- A amostra é aleatória
-
Pelo menos um dos seguintes é verdade:
- A população é normalmente distribuída
Para o item (b) precisamos do valor do escore correspondente ao nível de confiança de 95%:
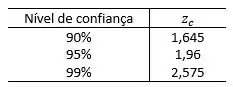
Como nosso nível de significância é de 95%, então .
E pelo enunciado temos que:
Logo:
Passo 3
(c) Construa um intervalo de confiança de 95% para a média populacional. Interprete os resultados.
Um intervalo de confiança para a média populacional é:
Limite inferior:
Limite superior:
Intervalo de confiança de 95% para a média populacional:
E ai galera, gostaram da resolução. Te aguardo em mais exercícios!
Resposta
(a)
(b)
(c)
Com 95% de confiança, podemos dizer que o tempo gasto assistindo a vídeos on-line a cada dia dos estudantes universitários está entre 5,989 e 7,707 minutos.