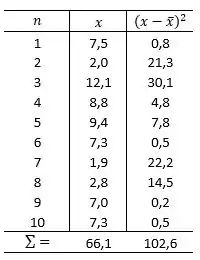
O conjunto de dados representa o tempo (em minutos) gasto verificando e-mail para uma amostra aleatória de funcionários de uma empresa.
![]()
(a) Calcule a média e o desvio padrão amostral.
(b) Construa um intervalo de confiança de 90% para a média populacional. Interprete os resultados. Suponha que os tempos são normalmente distribuídos.
(c) Repita a parte (b), supondo . Interprete e compare os resultados.
Passo 1
Oi galerinha, ansiosos para mais uma resolução? Vem comigo!
(a) Para o cálculo da média e do desvio padrão amostral iremos utilizar as seguintes equações:

Passo 2
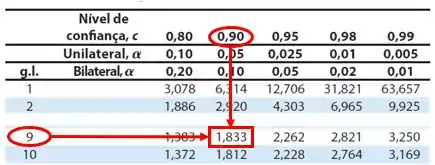
(b) Como já calculamos a média amostral no item (a), precisamos calcular a margem de erro E, para obtermos um intervalo de confiança de 90% (). E nosso desvio padrão populacional () é desconhecido, com uma população normalmente distribuída. Então precisamos encontrar os graus de liberdade () para obtermos o valor crítico ().
Temos que:
Pela Tabela da distribuição t:
Agora precisamos calcular a margem de erro :
Um intervalo de confiança para a média populacional é:
Limite inferior:
Limite superior:
Intervalo de confiança de 90% para a média populacional:
Com 90% de confiança, podemos dizer que o tempo médio populacional está entre 4,65 minutos e 8,57 minutos.
Passo 3
No item (c), o desvio padrão populacional é conhecido (), sendo assim, para este item precisamos encontrar o valor do escore:
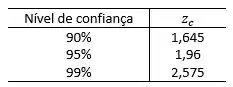
Como nosso nível de significância é de 90%, então .
Logo:
Limite inferior:
Limite superior:
Logo:
Com 90% de confiança, podemos dizer que o tempo médio populacional está entre 4,79 minutos e 8,43 minutos. Este intervalo de confiança é menor que do item (b).
Espero ter te ajudo, até mais!
Resposta
(a) ; .
(b) . Com 90% de confiança, podemos dizer que o tempo médio populacional está entre 4,65 minutos e 8,57 minutos.
(c) . Com 90% de confiança, podemos dizer que o tempo médio populacional está entre 4,79 minutos e 8,43 minutos. Este intervalo de confiança é menor que do item (b).