Considere um grafo com n vértices numerados de 1 a n e suponha que, entre cada um dos pares de vértices distintos, uma borda esteja presente com probabilidade p. O grau do vértice i, designado como , corresponde ao número de bordas que tem o vértice i como um de seus vértices.
(a) Qual é a distribuição de ?
(b) Determine , a correlação entre e .
Passo 1
Salve galera estudiosa, tudo certin??
Vamos para mais um problema de Probabilidade.

Afinal, o que são grafos?
É uma estrutura composta por um conjunto de pontos (vértices) e um conjunto de bordas que ligam esses pontos (arestas). Num grafo, entre dois vértices quaisquer pode haver ou não uma aresta e o grau de um vértice é definido como o número de arestas presentes naquele vértice. Como nas figuras abaixo:
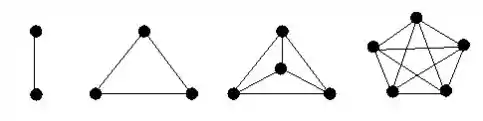
a) Nosso primeiro questionamento é de certo modo muito intuitivo, vejamos:
Em um grafo com n vértices, dado um vértice i pode haver nele uma aresta com qualquer um dos demais n-1 vértices restantes de modo independente e com a mesma probabilidade p, temos que. Essa é uma característica própria da função binomial.
Podemos concluir que então:
Passo 2
b) Vamos definir as variáveis aleatórias que irá indicar se existe uma aresta entre o vértice i e o vértice k e que irá indicar, da mesma forma, se há aresta entre os vértices j e k. Então:
Analisando a covariância entre e , temos, por definição que:
Por propriedade de covariância, temos que já que as variáveis são independentes.
E por se tratar de uma distribuição binomial temos que:
Logo,
Finalmente, a correlação entre as variáveis é dada por:
Onde, na distribuição binomial , assim:
Simplificando:
Resposta
a) Distribuição Binomial
b) Correlação: