Considere o seguinte jogo de dados: os jogadores 1 e 2 rolam um par de dados alternadamente. A banca então rola os dados para determinar o resultado de acordo com a seguinte regra: o jogador i, i = 1,2, vence se a sua jogada for estritamente maior do que a da banca. Para i = 1,2, considere
e mostre que I, e I, são positivamente correlacionadas. Explique por que esse resultado já era esperado
Passo 1
Salve galera estudiosa, tudo certin??
Vamos para mais um problema de Probabilidade.

Primeiramente, vamos definir como sendo o jogador 1, jogador e a banca, respectivamente. Nosso objetivo é mostrar que
Vale observar que:
E por propriedade de probabilidade, temos que:
Para calcular as duas probabilidades que surgiram no segundo membro da igualdade, faremos uso da lei da probabilidade total, daí teremos que:
Em outras palavras, a probabilidade (do jogador 1 obter pontuação estritamente maior que a banca é igual ao somatório do produto entre a probabilidade dele obter uma pontuação maior que a já obtida pela banca ( e a probabilidade da banca obter aquele dado resultado (.
De modo similar teremos que:
Agora que temos a expressão para determinar a probabilidade total, vamos calculá-la.
Passo 2
Vamos calcular as duas parcelas da probabilidade, sabendo que n = 6 pois é o número de faces do dado, então teremos:
Valendo lembrar que nesse caso a probabilidade de B é muito simples. Como a banca irá jogar dois dados, cada um com seis faces, o seu resultado será . Já a probabilidade do jogador ganhar está diretamente condicionada ao resultado da banca. No final, a expressão ficará assim.
Realizando a soma para cada valor de b = 1,2,3,4,5,6 obtemos:
De modo análogo, para o jogador 2 teremos o mesmo processo, e por simetria:
Assim, vamos obter que:
Passo 3
Vamos definir agora o valor de . Sabemos que dentro do conjunto de possibilidades ao lançar dois dados o menor resultado possível é 2 e o maior é 12. Para que o jogador obtenha a vitória o esperado é que ele possua um resultado acima da média entre 2 e 12, que no caso seria 7 pontos. Logo, .
Analisando a função de probabilidade da soma do lançamento de dois dados, temos a seguinte tabela:
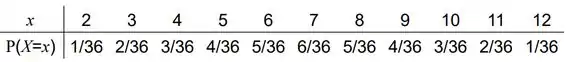 Assim:
Assim:
Portanto,
Assim, a expressão que desejávamos determinar fica assim:
Logo, como queríamos demonstrar.
Resposta
Este resultado era esperado, ema vez que, por exemplo, saber que o jogador 1 ganhou implica que o banco pode ter obtido um resultado muito baixo em seus dados, isso deixa espaço para o jogador 2 ganhar também. Logo, essas variáveis estão positivamente correlacionadas.