Consumo de leite
Você está realizando um estudo sobre consumo per capita de leite, por semana. Um estudo anterior descobriu que o consumo per capita de leite, por semana, era normalmente distribuído, com uma média de 48,7 onças líquidas e um desvio padrão de 8,6 onças líquidas. Você seleciona aleatoriamente 30 pessoas e registra o consumo semanal de leite mostrado a seguir.
40 45 54 41 43 31 47 30 33 37 48 57 52 45 38
65 25 39 53 51 58 52 40 46 44 48 61 47 49 57
(a) Construa um histograma de frequência para mostrar esses dados. Use sete classes. Os consumos parecem ser normalmente distribuídos? Explique.
(b) Calcule a média e o desvio padrão de sua amostra.
(c) Compare a média e o desvio padrão de sua amostra com a média e o desvio padrão do estudo anterior. Discuta as diferenças.
Passo 1
Fala aí galera, bora resolver o nosso exercício? Vamos lá, começando pela letra (a):
Bom, para começarmos, vamos trazer aqui os valores das vidas úteis dos pneus que foram dadas no enunciado:
48.778 41.046 29.083 36.394 32.302 42.787 41.972 37.229
- .920 38.030 38.445 30.750 38.886 36.770 46.049
Beleza. Com isso, vamos construir o nosso histograma analisando a frequência para as 5 classes de valores que são pedidas. Montando os valores numa tabela, vamos ter:
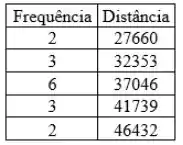
Se a gente utilizar os dados nossa tabela, o histograma vai ficar:
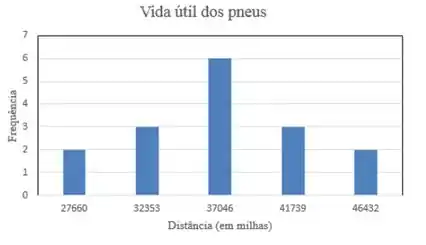
Pelo histograma, podemos perceber que a vida útil do pneu pode ser considerada como normalmente distribuída, pois podemos notar que ele possui uma simetria.
Passo 2
Show, agora vamos para a letra (b). Aqui vamos calcular a média e o desvio padrão da amostra.
Logo de cara, vamos montar aqui uma tabela com os valores de , suas variâncias e o desvio relacionado de cada valor:
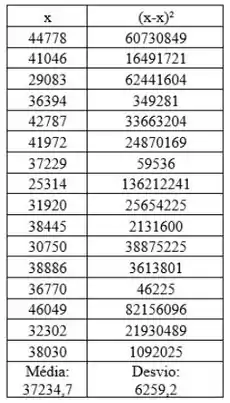
Pelos valores, podemos concluir então que o valor da média e do desvio padrão são:
Passo 3
Por fim, vamos para a letra (c).
Antes, vamos pegar aqui o valor da média e do desvio padrão fornecidos pelo fabricante:
E agora o que calculamos:
Se a gente analisar a vida útil média do pneu calculada, ela é inferior a fornecida pelo fabricante.
Analisando também o desvio padrão, podemos ver que o calculado é maior que o fornecido pelo fabricante.
Logo, concluímos que os pneus da amostra possuem um período de vida mais curto e tem uma variação maior que do que a afirmada pelo fabricante.