Distribuição uniforme. Uma distribuição uniforme é uma distribuição contínua de probabilidade para uma variável aleatória x definida no intervalo a ≤ x ≤ b, sendo todos os subintervalos de x, de mesmo comprimento, igualmente prováveis de ocorrer. O gráfico de uma distribuição uniforme é mostrado a seguir.

A função densidade de probabilidade de uma distribuição uniforme é:
no intervalo de a . Para qualquer valor de x menor que a ou maior que b, y = 0. Nos exercícios 59 e 60, use essa informação
Mostre que a função densidade de probabilidade de uma distribuição uniforme satisfaz as duas condições para uma função densidade de probabilidade.
Passo 1
Fala aí galera, bora resolver o nosso exercício? Vamos lá.
Primeiramente, precisamos ter em mente que a função densidade de probabilidade é utilizada para representar uma distribuição contínua de probabilidades. Ela deve satisfazer duas condições: a área total sob a curva deve ser igual à 1 e a função nunca pode ser negativa.
Show, vamos pegar o gráfico do enunciado e verificar cada condição:
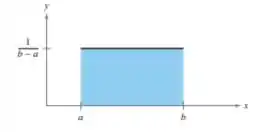
Para calcularmos a área do gráfico, vamos fazer:
Show, primeira condição satisfeita. Agora olhando para a segunda condição.
Repara que no gráfico , logo:
Com isso, o nosso gráfico não é negativo.
Logo, podemos afirmar que a função densidade de probabilidade de uma distribuição uniforme satisfaz as duas condições.