Encontre os valores críticos e para o nível de confiança e tamanho de amostra .
;
.
Passo 1
Oi pessoal, vem fazer esse exercício junto comigo!
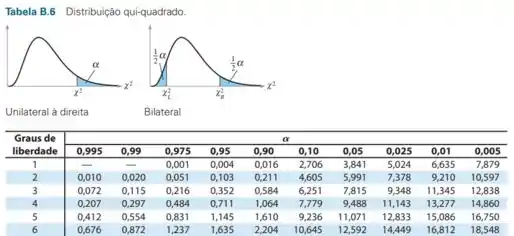
Iremos encontrar os graus de liberdade () e as áreas à direita de e , para encontrarmos seus valores críticos através da Tabela de distribuição qui-quadrado. Então, vamos lá!
Primeiramente precisamos calcular os graus de liberdade:
Os valores críticos de qui-quadrado ( e ) com um nível de confiança , são os que iremos consultar na Tabela, através das áreas à direita.
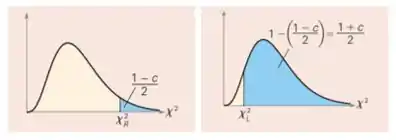
Passo 2
Com esses valores encontrados, que representam a curva qui-quadrado à direita (0,025 e 0,975) e os graus de liberdade (), iremos encontrar os valores críticos, da seguinte maneira:
Para :
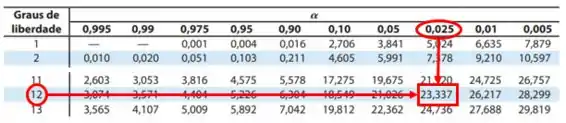
Para :
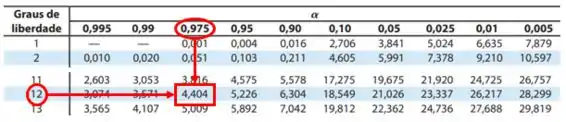
Então:
E ai pessoal, consegui te ajudar? Espero que sim! Até mais.