O exame “Western blot” é um teste sanguíneo para a presença do vírus HIV. Foi descoberto que esse teste dá, algumas vezes, resultados falsos positivos para HIV. Um pesquisador médico afirma que a taxa de falsos positivos é de 2%. Um estudo recente com 300 doadores de sangue americanos selecionados aleatoriamente, que não têm HIV, descobriu que 3 receberam resultado falso positivo no teste. Para o nível de significância , há evidência suficiente para rejeitar a afirmação do pesquisador? (Adaptado de: Centers for Disease Control and Prevention.)
- Identifique a afirmação e formule e ,
- Encontre o(s) valor(es) crítico(s) e identifique a(s) região(ões) de rejeição,
- Calcule a estatística de teste padronizada ,
- Decida se rejeita ou não rejeita a hipótese nula e
- Interprete a decisão no contexto da afirmação original.
Se for conveniente, use tecnologia.
Passo 1
Olá pessoal, vamos resolver esse exercício no estilo Responde Aí?! Vem comigo.
Com a afirmação de que “a taxa de falsos positivos é de 2%” conseguimos identificar nossas hipóteses nula e alternativa:
(afirmação);
.
Passo 2
Como o teste é bilateral e o nível de significância é , então:
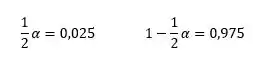
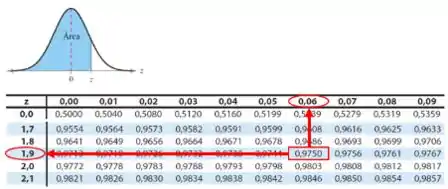
Os valores críticos são:
;
.
E as regiões de rejeição:
;
.
Passo 3
A estatística de teste padronizada é dada pela seguinte equação:
Para esse cálculo precisamos da proporção de não sucessos ():
E da proporção amostral ():
Onde:
;
.
Logo:
;
;
.
Como está fora da região de rejeição, então não rejeitamos
Resposta
- (afirmação);
- Os valores críticos são:
- .
- Não rejeita .
- Não há evidência suficiente, ao nível de significância de 5%, para rejeitar a afirmação de que a taxa de falsos positivos é de 2%.
.
;
.
E as regiões de rejeição:
;
.