Enunciado
Probabilidade e Estatística - Estatística Aplicada Farber e Larson- Ed: 6º - Capítulo 5.4 - Ex. 9
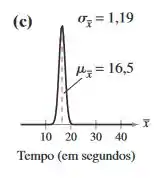
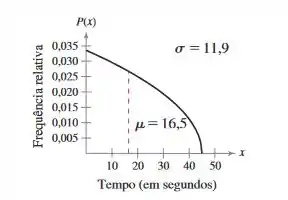
Nos exercícios 9 e 10, o gráfico de uma distribuição populacional é mostrado, com sua média e desvio padrão. Uma amostra de tamanho 100 é retirada da população. Determine qual dos gráficos indicados (a) a (c) mais se assemelharia à distribuição amostral das médias amostrais. Explique seu raciocínio.
O tempo de espera (em segundos) em um semáforo durante o sinal vermelho.
A -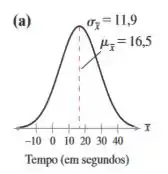 
Passo 1
Fala pessoal, tudo belezinha? vamos responder mais uma questão, então prepara o material e vamos responder!!!
Primeiramente, vamos anotar as variáveis que o enunciado nos dá, note que a média é dada pelo primeiro gráfico (média e desvio padrão no caso), seus respectivos valores são:
Primeiro ponto, como se tem uma quantidade relativamente grande de amostras, temos que pelo Teorema do Limite Central, o gráfico da população vai se assemelhar com a distribuição normal.
Passo 2
Beleza, já sabemos o motivo do gráfico da amostra ser uma distribuição normal, agora temos que descobrir quais os parâmetros dessa curva. Primeiro que a média não muda, então temos a seguinte característica:
Já no caso do desvio padrão, temos uma fórmula para esse caso:
Substituindo os valores, temos:
Passo 3
Logo, a média do gráfico será igual a 18,5 e o desvio padrão . O gráfico que mais se encaixa nesses dois parâmetros é o da letra c).
