Nos exercícios 11 a 14, determine a média e o desvio padrão da população. Liste todas as amostras (com reposição) do tamanho dado a partir daquela população e encontre a média de cada uma. Calcule a média e o desvio padrão da distribuição amostral das médias e compare-os com a média e o desvio padrão da população.
Os valores que quatro amigos pagaram pelos seus tocadores de MP3 são US$ 200, US$ 130, US$ 270 e US$ 230. Use um tamanho de amostra de 2.
Passo 1
Fala pessoal, belezinha? vamos responder mais uma questão, então prepara o material e vamos responder!
Vamos lá, primeiro passo aqui é fazer uma tabelinha bem básica em seu editor de planilhas.
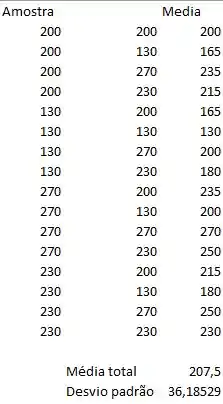
Pelos cálculos do software, a média é igual e o desvio padrão igual a
Passo 2
Agora, é botar a mão na massa e usar as fórmulas. A média é dada pela soma dos termos dividido pela quantidade de termos.
Substituindo os valores, temos:
Note que a média é exatamente a mesma.
Passo 3
Já no caso do desvio padrão, temos que usar uma fórmula, envolvendo raiz quadrada:
Note que o desvio padrão é maior quando se tem uma quantidade menor de amostras.