Nos exercícios 11 a 14, determine a média e o desvio padrão da população. Liste todas as amostras (com reposição) do tamanho dado a partir daquela população e encontre a média de cada uma. Calcule a média e o desvio padrão da distribuição amostral das médias e compare-os com a média e o desvio padrão da população.
As notas em um teste de três alunos em um grupo são 98, 95 e 93. Use um tamanho de amostra de 3.
Passo 1
Fala pessoal, tudo belezinha? vamos responder mais uma questão, então vamos lá responder!!!
Aqui, primeiro é necessário criar uma tabela para analisar a população toda do experimento, com isso temos a seguinte tabela:
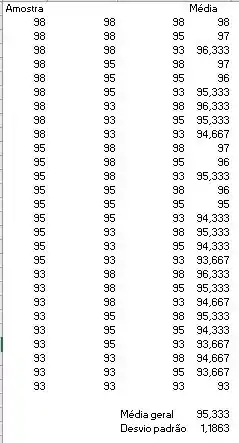
Com isso, temos que a média é igual a 95,33 e o desvio padrão vai ser igual a 1,1863 .
Passo 2
Agora é tirar a média e o desvio padrão da amostra, o enunciado nos diz que é uma amostra de 3 elementos, então vamos calcular a média primeiramente:
Enquanto o desvio padrão é igual a: