Nos exercícios 11 a 14, determine a média e o desvio padrão da população. Liste todas as amostras (com reposição) do tamanho dado a partir daquela população e encontre a média de cada uma. Calcule a média e o desvio padrão da distribuição amostral das médias e compare-os com a média e o desvio padrão da população.
As contagens de palavra de 5 redações são 501, 636, 546, 602 e 575. Use um tamanho de amostra de 2.
Passo 1
Fala pessoal, tudo belezinha? vamos responder mais uma questão, então prepara o material e vamos responder!
Vamo lá, a média no bruto é a soma de todos os valores dividindo pelo número de amostras, e o desvio padrão é a raíz quadrada da soma dos desvios dividido por n – 1. Mas assim pode parecer estranho, então vamos para fórmula:
E
Agora, vamos analisar a tabela da distribuição da amostra, ela vai gerar alguns resultados interessantes...
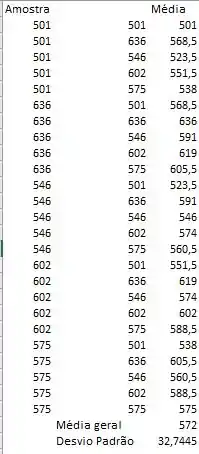
Essa tabela mostra que a população analisada tem uma média geral de 572 e desvio padrão igual a 32,7445.
Passo 2
Agora vamos para a amostra, sua média é gerada pelos parâmetros gerais, o que indica um cálculo mais simples para calcular a média, então pensa, o trabalho de gerar uma tabela será substituído por uma média de 5 número, não é ótimo? Sim, perfeito. Agora, isso acontece com o desvio padrão?
A média é dada por:
Já o desvio padrão é dado por:
Entendeu que a média será igual nos dois casos, mas o desvio padrão não será igual!
Resposta
Ei, a resposta está no passo a passo :)