Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Estatística Aplicada Farber e Larson- Ed: 6º - Capítulo 5.1 - Ex. 22

Nos exercícios 17 a 22, encontre a área da região indicada sob a curva normal padrão. Se for conveniente, use ferramentas tecnológicas para encontrar a área.

Passo 1

Fala pessoal, belezinha? vamos responder mais uma questão, então prepara o material e vamos resolver

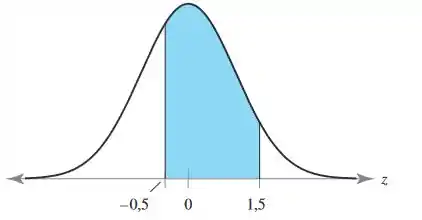
Esse problema será resolvido através da tabela, o motivo é que facilita por questões de tempo, nós já temos os intervalos definidos ( - 0,5   e   1,5 ) , agora é usar o fato que a área em azul será a probabilidade entre os intervalos de - 0,5 e 1,5 .

Podemos representar a probabilidade da seguinte forma:

P - 0,5 < Z < 1,5

A probabilidade P Z < - 0,5 pode ser encontrada analisando a tabela, (você pode verificar no apêndice do livro), linha em - 0,5 e coluna em 0,00 . De acordo com a tabela, temos que:

P Z < - 0,5 = 0,3085

No caso da probabilidade P ( Z < 1,5 ) , serve o mesmo processo, com linha em 1.5 e coluna em 0,00 . Com isso, temos:

P Z < 1,5 = 0,9332

Passo 2

Já descobrimos a probabilidade dos casos separados P Z < - 0,5   e   P ( Z < 1,5 ) . O caso de P - 0,5 < Z < 1,5 será a subtração entre os casos separados, logo:

P - 0,5 < Z < 1,5 = P Z < 1,5 - P Z < - 0,5

Substituindo os valores, temos:

P - 0,5 < Z < 1,5 = 0,9332 - 0,3085 = 0,6247

Resposta

P - 0,5 < Z < 1,5 = 0,6247