Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Estatística Aplicada Farber e Larson- Ed: 6º - Capítulo 5.1 - Ex. 21

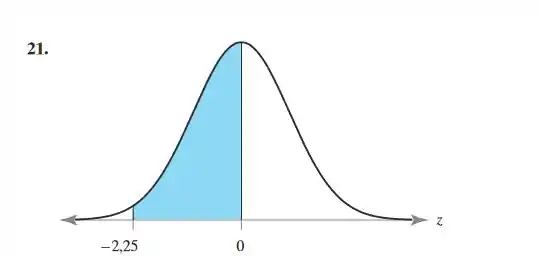
Nos exercícios 17 a 22, encontre a área da região indicada sob a curva normal padrão. Se for conveniente, use ferramentas tecnológicas para encontrar a área.

Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos lá!

Primeiramente, podemos perceber que a área é representada pela distribuição normal é entre ponto - 2,25 e 0 . Sendo que, essa área em azul representa a probabilidade, com isso, temos a seguinte probabilidade:

P - 2,25 < Z < 0

A probabilidade P Z <   - 2,25 pode ser encontrada pela tabela padrão de distribuições normais, usando a linha - 2,2   e a coluna 0,05 , usando a tabela temos que P é igual a:

P Z <   - 2,25 = 0,0122

Passo 2

Beleza, tudo certinho, agora é encontrar a probabilidade quando Z está entre - 2,25   e 0 . Vamos usar a tabela de novo, dessa vez a linha fica em 0,0   e a coluna em 0,00 . Com isso temos que a probabilidade será de:

P Z < 0 = 0,5000

Passo 3

Agora, você já percebeu que a probabilidade de P - 2,25 < Z < 0 é a probabilidade de P ( Z < 0 ) menor P ( Z < - 2,25 ) . Dado esses resultados, chegamos a seguinte conclusão:

P - 2,25 < Z < 0 = P Z < 0 - P ( Z < - 2,25 )

Substituindo os valores, temos:

P - 2,25 < Z < 0 = 0,5000 - 0,0122 = 0,4878

Resposta

P - 2,25 < Z < 0 = 0,4878