Nos exercícios 17 e 18, (a) construa uma distribuição binomial, (b) represente graficamente a distribuição binomial usando um histograma e descreva seu formato e (c) identifique quaisquer valores da variável aleatória x que você consideraria incomuns. Explique seu raciocínio.
Trinta e oito por cento das mulheres que trabalham fora, nos Estados Unidos, ganham mais que seus maridos. Você seleciona aleatoriamente cinco mulheres que trabalham fora, nos Estados Unidos, e pergunta se elas ganham mais do que seus maridos. A variável aleatória representa o número de mulheres americanas que trabalham fora e ganham mais do que seus maridos. (Fonte: U.S. Bureau of Labor Statistics.)
Passo 1
Fala aí galera, bora resolver o nosso exercício? Vamos lá, começando pela letra (a).
Antes de começarmos, temos que ter em mente que aqui para resolvermos o nosso exercício vamos construir a distribuição de probabilidade binominal, e para isso vamos usar a fórmula:
Além disso, importante relembrar que:
Logo:
Aonde que:
Show, pelo enunciado, vamos ver que:
Beleza, então vamos começar a calcular cada probabilidade:
E está construída a nossa distribuição de probabilidades.
Passo 2
Show, agora vamos para a letra (b). Aqui vamos representar as probabilidades calculadas no Passo 1 em formato de tabela:
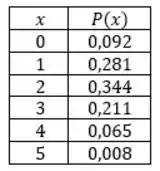
E com isso, podemos construir o nosso histograma:

Se a gente olhar o nosso histograma, reparem que nosso histograma é assimétrico, ele não é igualzinho de cada lado.
Nesse caso, ele sofre com uma distribuição assimétrica à direita.
Passo 3
E por fim, vamos para a letra (c). Aqui temos que verificar se há algo de incomum nos valores.
Antes de tudo, para termos um evento incomum, a probabilidade de acontecer deve ser menor que .
Se a gente for olhar para o nosso histograma:
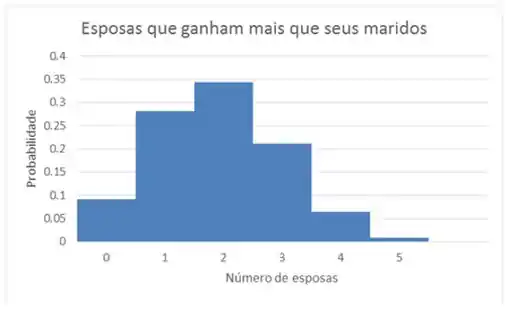
Reparem que o valor está bem abaixo de , logo ele é incomum.