Nos exercícios 19 a 24, construa o intervalo de previsão indicado e interprete os resultados.
Construa um intervalo de previsão de 90% para o tempo médio que as mulheres gastam, por dia, assistindo televisão no Exercício 10, quando o tempo médio que os homens passam , por dia, assistindo televisão é 4,2.
Passo 1
E aí pessoal, belezinha. Vamos com a revisão dos conteúdos de correlação e regressão!!!
O exercício pede para construirmos o intervalo de previsão: .
Seguindo as instruções do livro didático, temos que para n = 10, o número de graus de liberdade é: , e que a reta de regressão é dada por .
Passo 2
A partir do que sabemos vamos encontrar o valor crítico para 90% de confiança na tabela B.5 do apêndice B (página 556 do livro).
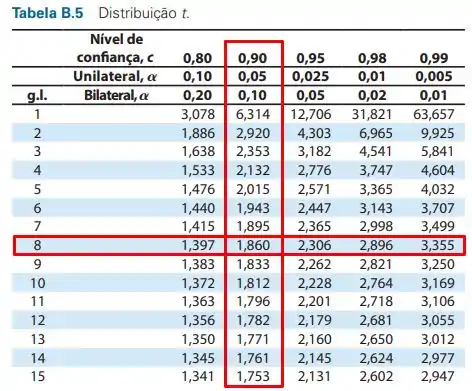
Para 8 graus de liberdade e 90% de confiança temos que tc = 1,860.
Passo 3
E como o erro padrão da estimativa não foi calculado no exercício 9, devemos encontarr o seu valor. Com o uso da tabela já construída, torna-se mais interessante utilizar a formulação (Ao invés de construir uma nova tabela com valores de previsão de y e os desvios), como segue:
Com a tabela do exercício 9, agora incluindo uam coluna para os quadrados de y, temos:
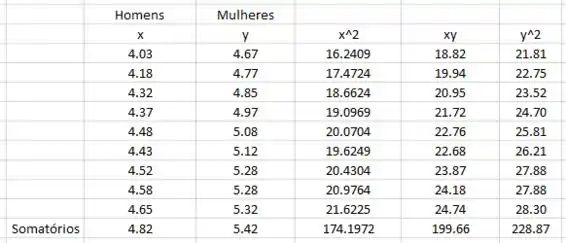
Daí podemos substituir na equação:
*Observação: Se possível façam os cálculos no Excel para minimizar a propagação de erros devido aos arredondamentos.
Passo 4
A margem de erro E é calculada pela expressão:
Para o uso dessa expressão temos que x0 = 4,2, mas devemos calcular a média de x:
Substituindo os valores calculados e os fornecidos, podemos calcular a margem de erro:
Passo 5
Para calcular a estimativa pontual para x = 4,2, usamos a reta de regressão dada:
Temos que os limites inferior e superior são dados por:
E o intervalo de previsão, com 90% de confiança é dado por:
Resposta
Ver passo a passo.