Nos exercícios 5 a 8, (a) determine a frequência esperada para cada célula na tabela de contingência, (b) identifique a afirmação e formule H0 e Ha , (c) determine os graus de liberdade, determine o valor crítico e identifique a região de rejeição, (d) calcule a estatística de teste qui-quadrado, (e) decida se rejeita ou não a hipótese nula e (f) interprete a decisão no contexto da afirmação original. Se for conveniente, use tecnologia.
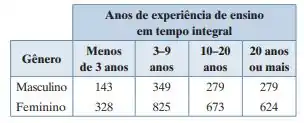
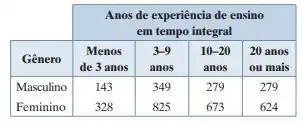
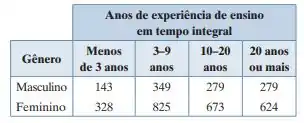
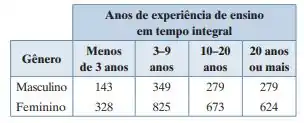
A tabela de contingência a seguir mostra os resultados de uma amostra aleatória de professores de escolas públicas do ensino fundamental e médio, por gênero e anos de experiência de ensino em tempo integral. Com a = 0,01, você pode concluir que o gênero está relacionado aos anos de experiência de ensino em tempo integral? (Adaptado de: U.S. National Center for Education Statistics.)
Passo 1
Fala aí galera, bora resolver o nosso exercício? Vamos lá, começando pela letra (a)
Aqui vamos calcular a frequência esperada para cada célula na tabela. Para isso, vamos usar a fórmula
Se a gente pegar a nossa tabela,
Vamos começar a calcular cada uma:
Passo 2
Show, agora vamos para a letra (b). Para formularmos as hipóteses, basta escrever de acordo com as variáveis do problema.
As hipóteses para o teste de independência são:
Passo 3
Agora vamos para a letra (c). O grau de liberdade é determinado de acordo com o número de linhas (r) e o número de colunas (c).
Logo, teremos:
Com o nível de significância de 1% e 3 graus de liberdade, o valor crítico será e a região crítica será .
Passo 4
Agora vamos para a letra (d). A estatística de teste será calculada com as frequências esperadas calculadas no Passo 1 e observadas que estão presentes na tabela.
Vamos calcular usando a fórmula:
Usando a frequência esperada calculada com o valor da tabela de acordo com a coordenada da frequência esperada, somando tudo vamos encontrar:
Portanto, a estatística de teste resulta em .
Passo 5
Show, vamos para a letra (e). Para decidir se rejeitamos , basta verificar se a estatística de teste pertence a região crítica.
Como
Passo 6
Por fim, vamos para a letra (f). Para interpretarmos a decisão, vamos usar as informações que encontramos no exercício.
Portanto, não há evidências suficientes, ao nível de 1% de significância, para concluir que os anos de experiência de ensino em tempo integral são dependentes do gênero.