Nos exercícios 17 a 20, (a) identifique a afirmação e formule H0 e Ha , (b) determine o valor crítico e identifique a região de rejeição, (c) calcule a estatística de teste F, (d) decida se rejeita ou não rejeita a hipótese nula e (e) interprete a decisão no contexto da afirmação original. Suponha que as amostras são aleatórias e independentes e as populações normalmente distribuídas. Se for conveniente, use tecnologia.
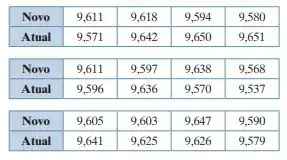
Um técnico de qualidade afirma que a variância dos diâmetros de inserção produzidos pelo novo molde de injeção para inserção de painel de automóvel é menor que a variância dos diâmetros de inserção produzidos pelo molde atual. A tabela a seguir apresenta amostras de diâmetros de inserção (em centímetros) para os moldes novo e atual. Com a = 0,05, você pode concordar com a afirmação do técnico?
Passo 1
Fala aí galera, bora resolver o nosso exercício? Vamos lá, começar pela letra (a):
Para elaborar as hipóteses, precisamos identificar as afirmações sobre as variâncias informadas no exercício. Dessa forma, as hipóteses do teste serão:
Passo 2
Show, agora vamos para a letra (b). O exercício já nos informou tanto o nível de significância quanto os graus de liberdade do denominador e numerador. Logo, basta encontrar o valor crítico na tabela F.
Por inspeção, o valor crítico será e a região crítica
Passo 3
Show, agora vamos para a letra (c). Primeiramente, devemos calcular as médias das amostras:
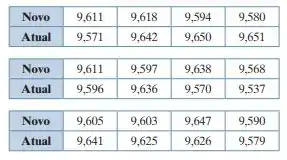
Ok, médias calculadas. Com elas, vamos agora calcular as variâncias. Para isso, vamos a fórmula:
Aonde é um dos dados da tabela e o número total de dados:
E finalmente, com as variâncias calculadas, a gente consegue calcular a estatística de teste:
Passo 4
Show, agora vamos para a letra (d). Para concluirmos o teste, basta utilizar os dados obtidos nas partes (b) e (c).
Perceba que , logo podemos rejeitar .
Passo 5
Por fim, vamos para a letra (e). Vamos concluir a resolução do problema
Portanto, há evidências, supondo 5% de significância, que a variância do diâmetro de inserção produzido pelo atual molde de injeção é maior que o novo.