Nos exercícios 1 a 4, (a) identifique a distribuição esperada e formule H0 e Ha , (b) determine o valor crítico e identifique a região de rejeição, (c) determine a estatística de teste quiquadrado, (d) decida se rejeita ou não rejeita a hipótese nula e (e) interprete a decisão no contexto da afirmação original.
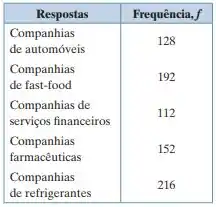
Uma organização afirma que a opinião de adultos com 55 anos ou mais sobre qual indústria tem a propaganda mais confiável é uniformemente distribuída. Para testar essa afirmação, você seleciona aleatoriamente 800 adultos com 55 anos ou mais e pergunta qual indústria tem a propaganda mais confiável. A tabela a seguir mostra os resultados. Para a = 0,05, teste a afirmação da organização. (Adaptado de: Harris Interactive.)
Passo 1
Fala aí galera, bora resolver o nosso exercício? Vamos lá.
Primeiramente, precisamos ter em mente que a hipótese nula é: “A opinião de adultos com 55 anos ou mais sobre qual indústria tem a propaganda mais confiável é uniformemente distribuída.”, que representa a própria afirmação.
Com isso, podemos concluir que a hipótese alternativa é: “A opinião de adultos com 55 anos ou mais sobre qual indústria tem a propaganda mais confiável não é uniformemente distribuída.”
Passo 2
Show, agora vamos para a letra (b). Vamos calcular o valor crítico e identificar a região de rejeição.
Pelo gráfico, nós temos 5 categorias, então a distribuição qui-quadrado tem:
Com isso, conseguimos localizar na tabela B.6, utilizando e
Logo, por meio da tabela podemos afirmar que o valor crítico é e que a região de rejeição é .
Passo 3
Agora vamos para a letra (c). Vamos construir uma tabela com as frequências observadas e esperadas.
Como o enunciado nos diz que a distribuição é uniforme, então as frequências esperadas são todas iguais, logo:
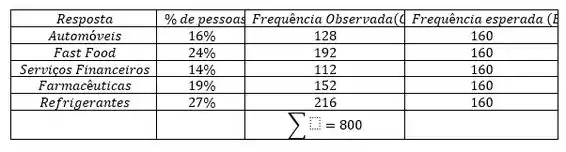
Agora, vamos calcular o valor da estatística de teste padronizada.

Logo, o valor da estatística de teste padronizada é
Passo 4
Agora vamos para a letra (d). Agora, nós só devemos rejeitar a hipótese nula, se o valor da estatística de teste padronizada for maior que o valor crítico
Sabendo que:
Logo, como , então devemos rejeitar a hipótese nula .
Passo 5
Por fim, vamos para a letra (e).
Agora, como a hipótese nula não deve ser rejeitada, então não podemos aceitar a afirmação da organização.
Logo, podemos afirmar que não há evidências suficientes ao nível de significância de , para aceitarmos a afirmação de que a organização, de que a opinião de adultos com 55 anos ou mais sobre qual indústria tem a propaganda mais confiável é uniformemente distribuída.