Um fabricante de barras de cereais afirma que o desvio padrão do número de gramas de carboidratos em uma barra é de 1,11 grama. Uma amostra aleatória de 26 barras tem um desvio padrão de 1,19 grama. Para , há evidência suficiente para rejeitar a afirmação do fabricante? Suponha que a população é normalmente distribuída.
Para este teste, faça o seguinte:
- Identifique a afirmação e formule e .
- Determine se o teste de hipótese é unilateral à esquerda, unilateral à direita ou bilateral e se deve usar um teste , um teste ou um teste qui-quadrado. Explique seu raciocínio.
- Escolha uma das opções. Se for conveniente, use tecnologia.
- Decida se rejeita ou não rejeita a hipótese nula.
- Interprete a decisão no contexto da afirmação original.
Opção 1: Encontre o(s) valor(es) crítico(s), identifique a(s) região(ões) de rejeição e calcule a estatística de teste padronizada apropriada.
Opção 2: Calcule a estatística de teste padronizada apropriada e o valor .
Passo 1
Oi pessoal, vem comigo que irei te ajudar com este probleminha!
Do enunciado temos que:
;
;
;
.
Como a população é normalmente distribuída e com a afirmação do fabricante de barras de cereais de que “o desvio padrão do número de gramas de carboidratos em uma barra é de 1,11 grama” conseguimos formular as hipóteses:
(afirmação);
.
Como a hipótese alternativa () contém , então o teste é bilateral. Como o teste é para um desvio padrão e a população é normalmente distribuída, então utilizaremos o teste qui-quadrado.
Passo 2
Como o teste é bilateral, então para um nível de significância de :

E os graus de liberdade:
Então:
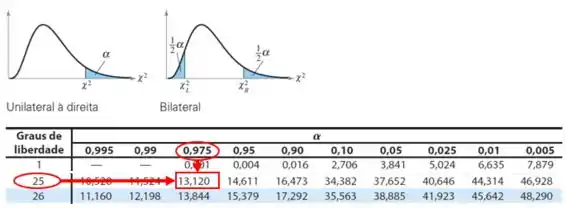

Os valores críticos são:
;
.
E as regiões de rejeição:
;
.
Passo 3
Agora iremos calcular a estatística de teste padronizada , pela seguinte equação:
Como está fora da região de rejeição, então não rejeitamos a hipótese nula (). Não há evidência suficiente, ao nível de significância de 5%, para rejeitar a afirmação do fabricante de barras de cereais de que o desvio padrão do número de gramas de carboidratos em uma barra é de 1,11 grama.
Consegui te ajudar? Espero que sim, até mais!
Resposta
- (afirmação);
- O teste é bilateral, porque a hipótese alternativa () contém . Utilizaremos o teste qui-quadrado, porque o teste é para um desvio padrão e a população é normalmente distribuída.
- Os valores críticos são:
- Não rejeita .
- Não há evidência suficiente, ao nível de significância de 5%, para rejeitar a afirmação do fabricante de barras de cereais de que o desvio padrão do número de gramas de carboidratos em uma barra é de 1,11 grama.
.
;
.
E as regiões de rejeição:
;
.
Estatística de teste padronizada :
.