Um fabricante de fornos de micro-ondas anuncia que menos de 10% de seus micro-ondas precisam de conserto durante os primeiros 5 anos de uso. Em uma amostra aleatória de 57 micro-ondas que têm 5 anos, 13% precisaram de conserto. Para , você pode concordar com a afirmação do fabricante? (Adaptado de: Consumer Reports.)
Para este teste, faça o seguinte:
- Identifique a afirmação e formule e .
- Determine se o teste de hipótese é unilateral à esquerda, unilateral à direita ou bilateral e se deve usar um teste , um teste ou um teste qui-quadrado. Explique seu raciocínio.
- Escolha uma das opções. Se for conveniente, use tecnologia.
- Decida se rejeita ou não rejeita a hipótese nula.
- Interprete a decisão no contexto da afirmação original.
Opção 1: Encontre o(s) valor(es) crítico(s), identifique a(s) região(ões) de rejeição e calcule a estatística de teste padronizada apropriada.
Opção 2: Calcule a estatística de teste padronizada apropriada e o valor .
Passo 1
Oie pessoal, espero que estejam bem! Vamos resolver esse exercício juntos? Vamos lá!
Do enunciado temos que:
;
;
;
.
Primeiramente iremos verificar se a distribuição amostral de pode ser aproximada por uma distribuição normal, para isso, precisamos que e .
Então:
Ambos os produtos e são maiores que 5, sendo assim podemos usar o teste e definir as hipóteses nula e alternativa, através da afirmação de um fabricante de fornos de micro-ondas de que “menos de 10% de seus micro-ondas precisam de conserto durante os primeiros 5 anos de uso”, logo:
;
(afirmação).
Como a hipótese alternativa () contém , então o teste é unilateral à esquerda. E utilizaremos o teste , porque e .
Passo 2
Como o teste é unilateral à esquerda e o nível de significância é :
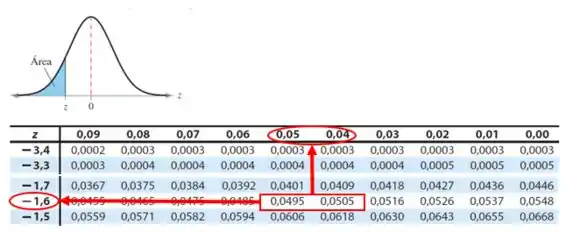
Teremos que interpolar os valores, onde:
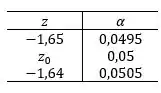
Interpolando:
O valor crítico é:
.
E a região de rejeição:
.
Passo 3
Agora iremos calcular a estatística de teste padronizada pela seguinte equação:
Como está fora da região de rejeição, então não rejeitamos Não há evidência suficiente, ao nível de significância de 5%, para suportar a afirmação do fabricante de que menos de 10% de seus micro-ondas precisam de conserto durante os primeiros 5 anos de uso.
Te espero para fazermos mais exercícios juntos!
Resposta
- ;
- O teste é unilateral à esquerda, porque a hipótese alternativa () contém . Utilizaremos o teste , porque e .
- O valor crítico é:
- Não rejeita .
- Não há evidência suficiente, ao nível de significância de 5%, para suportar a afirmação do fabricante de que menos de 10% de seus micro-ondas precisam de conserto durante os primeiros 5 anos de uso.
(afirmação).
.
E a região de rejeição:
.
Estatística de teste padronizada :
.