Faça estes problemas como se estivesse fazendo em sala. Depois, compare suas respostas com as respostas dadas no final do livro. Para cada exercício, siga as instruções a seguir.
(a) Identifique a afirmação e formule H0 e Ha .
(b) Determine o valor crítico e identifique a região de rejeição.
(c) Calcule a estatística de teste.
(d) Decida se rejeita ou não a hipótese nula.
(e) Interprete a decisão no contexto da afirmação original.
Se for conveniente, use tecnologia.
Nos exercícios 1 e 2, use a tabela a seguir, que lista a distribuição do grau de instrução para pessoas nos Estados Unidos com 25 anos ou mais. Ela também apresenta os resultados de uma pesquisa aleatória para duas faixas etárias adicionais. (Adaptado de: U.S. Census Bureau.)
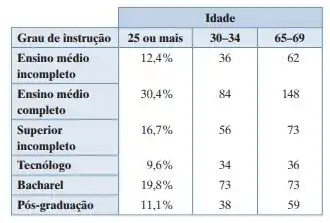
A distribuição para as pessoas nos Estados Unidos com 25 anos ou mais difere da distribuição para as pessoas nos Estados Unidos que têm entre 30 e 34 anos? Use a = 0,05.
Passo 1
Fala aí galera, bora resolver o nosso exercício? Vamos lá.
Primeiramente, precisamos ter em mente que a hipótese nula é: “A distribuição do grau de instrução para pessoas nos Estados Unidos com idade no intervalo de 30-34 anos é 12,4% com ensino médio incompleto; 30,45 com ensino médio completo; 16,7% com ensino superior incompleto; 9,6% com grau de tecnólogo; 19,8% com grau de bacharel e 11,1% com pós-graduação.”
E por fim, podemos concluir que a hipótese alternativa é: “A distribuição do grau de instrução para pessoas nos Estados Unidos com idade no intervalo de 30-34 anos difere da distribuição esperada”, que representa a própria afirmação.
Passo 2
Show, agora vamos para a letra (b). Vamos calcular o valor crítico e identificar a região de rejeição.
Pela tabela, nós temos 6 categorias, então a distribuição qui-quadrado tem:
Com isso, conseguimos localizar na tabela B.6, utilizando e
Logo, por meio da tabela podemos afirmar que o valor crítico é e que a região de rejeição é .
Passo 3
Agora vamos para a letra (c). Vamos construir uma tabela com as frequências observadas e esperadas:
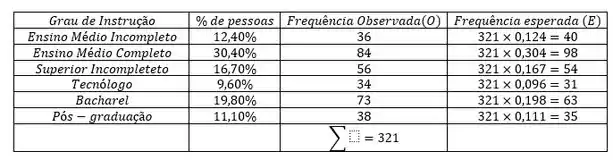
Agora, vamos calcular o valor da estatística de teste padronizada.
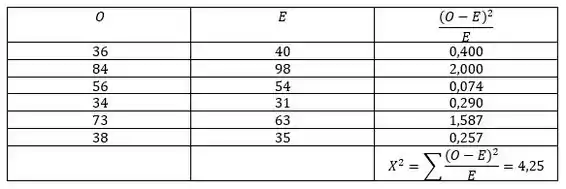
Logo, o valor da estatística de teste padronizada é
Passo 4
Agora vamos para a letra (d). Agora, nós só devemos rejeitar a hipótese nula, se o valor da estatística de teste padronizada for maior que o valor crítico
Sabendo que:
Logo, como , então não devemos rejeitar a hipótese nula .
Passo 5
Por fim, vamos para a letra (e).
Agora, como a hipótese nula não deve ser rejeitada, então não podemos afirmar que a distribuição para pessoas nos Estados Unidos com idades entre 30-34 anos é diferente de pessoas com 25 anos ou mais.
Logo, podemos afirmar que não há evidências suficientes ao nível de significância de , para aceitarmos a afirmação de que a distribuição para pessoas nos Estados Unidos com idades entre 30-34 anos é diferente de pessoas com25 anos ou mais.