Graduados na faculdade
Cerca de 35% dos trabalhadores americanos são graduados na faculdade. Você seleciona aleatoriamente 500 trabalhadores americanos e pergunta se eles são graduados na faculdade. Calcule a probabilidade de que o número dos que graduaram na faculdade seja (a) exatamente 175, (b) não mais que 225, (c) no máximo 200 e (d) identifique quaisquer eventos incomuns. Explique. (Fonte: U.S. Bureau of Labor Statistics.)
Passo 1
Salve, fera! Tudo bem? Essa questão pode não ser tão simples. Vamos encará-la juntos?
A partir do enunciado do problema, temos que:
Vamos analisar se esses dados satisfazem todos critérios para usarmos a aproximação de uma distribuição normal para uma aproximação binomial, onde .
Assim, temos:
Como os critérios foram satisfeitos, podemos então, usar a distribuição normal.
Determinando a média e o desvio padrão, temos:
Passo 2
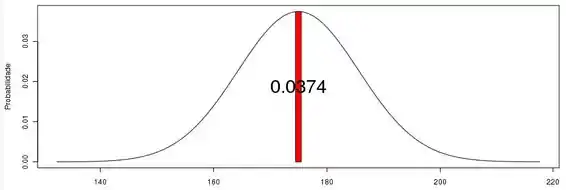
(a) Usando a correção de continuidade, a probabilidade discreta pode ser escrita como a probabilidade contínua . Calculando o valor escore-z, temos:
Portanto,
Da tabela de distribuição normal, temos: e , assim:
Através de software, encontramos o seguinte esboço e probabilidade:
Passo 3
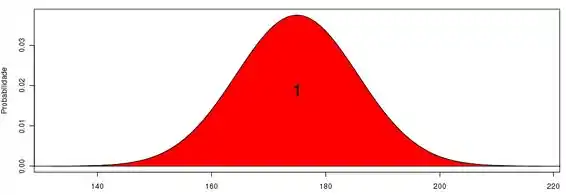
(b) Usando a correção de continuidade, a probabilidade discreta pode ser escrita como a probabilidade contínua . Calculando o valor escore-z, temos:
Portanto,
Da tabela de distribuição normal, temos: assim:
Através de software, encontramos o seguinte esboço e probabilidade:
Passo 4
(c) Usando a correção de continuidade, a probabilidade discreta pode ser escrita como a probabilidade contínua . Calculando o valor escore-z, temos:
Portanto,
Da tabela de distribuição normal, temos: assim:
Através de software, encontramos o seguinte esboço e probabilidade:
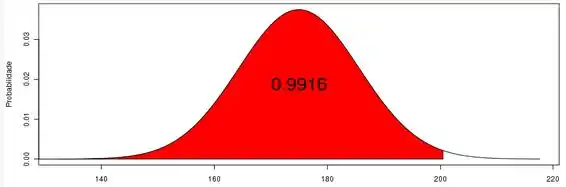
(d) O evento (a) é considerado incomum, uma vez que apresenta probabilidade menor que 5%.
Espero ter ajudado! Abraços e até a próxima!

Resposta
a) 3,98%. Consulte o esboço acima.
b) 100%. Consulte o esboço acima.
c) 99,16%. Consulte o esboço acima.
d) Os eventos (a) é incomum, pois apresenta probabilidade menor que 5%.