Um jogo popular nos cassinos de Nevada é o Keno, que é jogado da seguinte maneira: 20 números de 1 a 80 são sorteados aleatoriamente pelo cassino. Um apostador pode selecionar de 1 a 15 números; ele ganha se alguma fração dos números que escolheu for igual a qualquer um dos 20 números sorteados pela 'asa. O prêmio é função do número de elementos selecionados pelo apostador e do número de acertos obtido. Por exemplo, se o apostador selecionar apenas l número, então ele ou ela vence se este número estiver entre o conjunto de 20 números sorteados, e o prêmio é de R$2,20 para cada real apostado (como a probabilidade de o apostador ganhar é nesse caso igual a & é claro que o prêmio "justo" deveria ser R$3,00 para cada real apostado). Quando o jogador seleciona 2 números, um prêmio de R$12,00 é dado para cada real apostado se ambos os números estiverem entre os 20.
a) Qual seria o prêmio justo neste caso? Suponha que P, represente a probabilidade de que exatamente k dos n números escolhidos pelo apostador estejam entre os 20 selecionados pela casa.
b) Calcule P,,,.
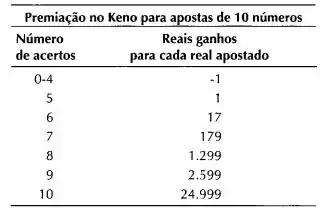
c) A aposta mais comum no Keno consiste na seleção de 10 números. Para tal aposta, o cassino distribui prêmios de acordo com a tabela a seguir. Calcule o prêmio esperado:
Passo 1
Fala galeraaa!
Vamos que vamos!
a)
O jogador escolheu 2 números. Suponha que ele tenha escolhido números que foram escolhidos pelo sistema. A probabilidade de fazer isso é de:
entāo a recompensa justa seria para cada R$ 1,00.
b)
Digamos que o jogador escolha n números, onde n é um número entre 1 e 15. A probabilidade de que ele tenha adivinhado exatamente para números é de:
Observe que este problema tem natureza hipergeométrica.
c)
Aqui temos n = 10. Define S como a variável aleatória que marca o retorno. O retorno esperado é
Insira os dados fornecidos na tabela e calcule SS. Onde , k é dado em (b). Assim, o retorno esperado e - 0, 206
Resposta
Veja a solução.