O procedimento de classificação descrito no Exercício 35 é algo assimétrico, porque a menor observação recebe posto 1 enquanto a maior recebe posto 2 e assim por diante. Suponha que ambas, a menor e a maior, recebam o posto 1, a segunda menor e a segunda maior recebam posto 2 e assim sucessivamente, e seja a soma dos postos. A distribuição nula de não é idêntica à distribuição nula de , portanto tabelas diferentes são necessárias. Considere o caso e . Liste todas as 35 possibilidades de ordenação dos três valores de entre as sete observações (por exemplo, 1, 3,7 ou ), atribua postos da maneira descrita, calcule o valor de para cada possibilidade e então tabele a distribuição nula de . Para o teste que rejeita se , qual valor de está associado a um nível de teste de aproximadamente 0,10? Este é o teste de Ansari-Bradley; para obter informações adicionais, veja o livro de Hollander e Wolfe na Bibliografia do capítulo.
Passo 1
E aí pessoal partiu para mais uma questão de (probabilidade)? Abaixo começaremos trazendo algumas informações do enunciado:
As únicas classificações possíveis agora são 1,2,3 e 4 . Cada rank triplo é obtido da ordenação X correspondente pelo "código" 1=1,2=2,3=3,4=4,5=3,6=2,7=1 (portanto, por exemplo, a ordenação X 256 corresponde para as posições 2,3,2).
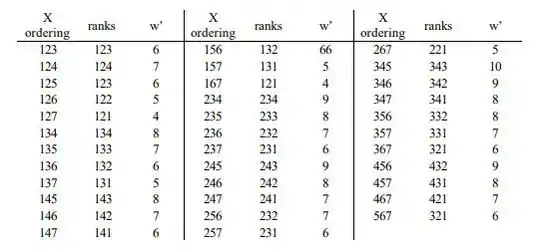
Como quando é verdadeiro, a probabilidade de qualquer ordenação particular é 1/35, obtemos facilmente a distribuição nula e os valores críticos dados na seção de resposta.
Resposta
Como quando é verdadeiro, a probabilidade de qualquer ordenação particular é 1/35, obtemos facilmente a distribuição nula e os valores críticos dados na seção de resposta.
Espero que tenham aprendido com essa questão, até a próxima !